题目内容
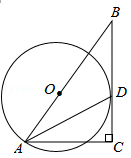
已知BC为半圆O的直径,AB=AF,AC交BF于点M,过A点作AD⊥BC于D,交BF于E,求证:AE=BE.
见解析
解析试题分析:首先根据AB=AF,得到弧相等,根据同弧所对的圆周角相等得到∠ABE=∠ACB,然后根据垂直的定义得到∠ACB=∠BAD,根据等式的性质得出∠ABE=∠BAD,从而说明AE=BE.
试题解析:∵AB=AF ∴弧AB=弧AF ∴∠ABE=∠ACB ∵BC为圆O的直径 ∴∠BAC=90°
又∵AD⊥BC ∴∠ACB+∠DAC=∠BAD+∠DAC=90° ∴∠ACB=∠BAD ∴∠ABE=∠BAD ∴AE=BE.
考点:同弧所对的圆周角相等、等腰三角形的判定.

练习册系列答案
相关题目
如图,AB是⊙O的直径,点C在⊙O上,若∠A=40°,则∠B的度数为( )
| A.80º | B.60º | C.50º | D.40º |


 CD于点E.连接AC、OC、BC.
CD于点E.连接AC、OC、BC.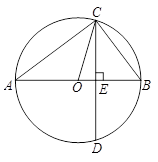

 的半径为4,
的半径为4, 是⊙
是⊙ ,且
,且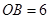 ,延长
,延长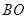 交⊙
交⊙ ,点
,点 为⊙
为⊙ 的垂线,垂足为
的垂线,垂足为 ,
, 平分
平分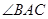 .
.
 是⊙
是⊙ 的长.
的长.