题目内容
12．
如图，AB，DE是⊙O的直径，点C是⊙O上的一点，且$\widehat{AD}$=$\widehat{CE}$，求证：BE=CE．
分析 根据对顶角相等得到∠AOD=∠BOE，再根据圆心角、弧、弦的关系得$\widehat{AD}$=$\widehat{BE}$，加上$\widehat{AD}$=$\widehat{CE}$，所以$\widehat{BE}$=$\widehat{CE}$，进一步得到BE=CE．
解答 答：BE=CE．理由如下：
证明：∵AB、DE是⊙O的直径，
∴∠AOD=∠BOE，
∴$\widehat{AD}$=$\widehat{BE}$，
∵$\widehat{AD}$=$\widehat{CE}$，
∴$\widehat{BE}$=$\widehat{CE}$，
∴BE=CE．
点评 本题考查了圆心角、弧、弦的关系：在同圆和等圆中，相等的圆心角所对的弧相等，所对的弦也相等．在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等．
练习册系列答案
53天天练系列答案
相关题目
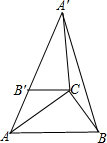如图．在Rt△ABC中，∠ABC=90°，∠B=60°，BC=2，△A′B′C是由△ABC绕点C顺时针旋转得到的，其中点A′与点A是对应点，点B?与点B是对应点，已知A，B′，A′在同一条直线上．
如图，已知直线l1：y=3x+1和直线l2：y=mx+n交于点P（-2，a），根据以上信息解答下列问题：
如图，正方形OABC顶点AC分别在x轴y轴正半轴上A（m，0）且m是分式方程$\frac{2}{x}$=$\frac{3}{x+1}$的解，OB=$\sqrt{2}$OA．