Question

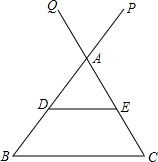如图，△ABC中，AB=20，BC=21，AC=13，如果动点D以每秒2个单位长的速度从点B出发沿射线BA方向运动，当运动到12秒时停止，直线DE∥BC，E为直线DE与直线CA的交点，若点D运动时间设为t秒．
（1）求当点D在线段AB上时线段DE的长度（用含t的代表式表示）；
（2）求出△DEC的面积S与时间t的函数关系式；
（3）S是否有最大值？若有，请求出最大值和相应t的值；若没有，请说明理由．

Answer 1

分析：（1）根据DE∥BC推出△ADE∽△ABC，得出

DE

21

=

20-2t

20

，求出即可；
（2）分为三种情况：①当0＜t＜10时，如图1，过点D作DM⊥BC于点M，作AN⊥BC于点N，由勾股定理求出BN=16，AN=12，推出△BDM∽△BAN，得出比例式，求出DM=

6

5

t，根据S=

1

2

×DE×DM，代入求出S=-

63

50

t²+

63

5

t；②当10＜t≤12时，根据△BAN∽△BDM得出比例式，代入求出DM=

6

5

t，根据△DEA∽△BAC汽车DE=

21

10

t-21，求出S=

63

50

t²-

63

5

t；③当D与A重合时，2t=20，求出t=10，S=S_△ABC；
（3）求出三种情况的最大值即可．

解答：解：（1）根据题意得：BD=2t，
当点D在线段AB上时，AD=AB-BD=20-2t，
∵DE∥BC，
∴△ADE∽△ABC，
∴

DE

BC

=

AD

AB

，
即

DE

21

=

20-2t

20

，
解得：DE=21-

21

10

t；

（2）①当0＜t＜10时，如图1，过点D作DM⊥BC于点M，作AN⊥BC于点N，
由勾股定理得：AN²=20²-BN²=13²-（21-BN）²，
BN=16，AN=12，
∴DM∥AN，
∴△BDM∽△BAN，
∴

BD

AB

=

DM

AN

，即

2t

20

=

DM

12

，
DM=

6

5

t，
S=

1

2

×DE×DM=

1

2

•（21-

21

10

t）•

6

5

t
S=-

63

50

t²+

63

5

t；
②当10＜t≤12时，如图2，
∵AN∥DM，
∴△BAN∽△BDM，
∴

BD

AB

=

DM

AN

，即

2t

20

=

DM

12

，
DM=

6

5

t，
∵DE∥BC，
∴△DEA∽△BAC，
∴

DE

BC

=

AD

AB

，

DE

21

2t-20

20

，
DE=

21

10

t-21，
S=

1

2

×DE×DM=

1

2

•（

21

10

t-21）•

6

5

t
S=

63

50

t²-

63

5

t；
③当D与A重合时，2t=20，
解得：t=10，
S=S_△ABC=

1

2

×BC×AN=

1

2

×21×12=126；
即S=

- 63 50 t2+ 63 5 t(0＜t＜10) 63 50 t2- 63 5 t(10＜t≤12) 126(t=10)

；

（3）S有最大值，
理由是：①当0＜t＜10时，S=-

63

50

t²+

63

5

t=-

63

50

（t-5）²+31.5；
当t=5时，此时S的最大值是31.5，
②当10＜t≤时，
S=

63

50

t²-

63

5

t=

63

50

（t-5）²-31.5，
抛物线的开口向上，在对称轴的右侧，s随t的增大，当t取12时，S最大，最大值是30.24
③当D与A重合时，2t=20，
解得：t=10，
S=S_△ABC=

1

2

×BC×AN=

1

2

×21×12=126；
综合上述，当t=10时，S最大，最大值是126．

点评：本题考查了相似三角形的性质和判定，二次函数的解析式，二次函数的最值，三角形的面积等知识点的综合运用，题目难度偏大．