题目内容
如图，两建筑物水平距离为32米，从点A测得对点C的俯角为30°，对点D的俯角为45°，则建筑物CD的高约为
- A.14米
- B.17米
- C.20米
- D.22米
A
分析：延长DC、交AE与E，则根据AE和∠EAC可以计算EC的长度，根据AE和∠EAD可以计算DE的长度，根据DE、CE的值即可计算CD的值，即可解题．
解答：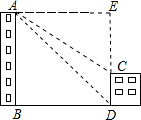
解：延长DC、交AE与E，
∠EAC=30°，∠EAD=45°，
∴CE=AE•
=
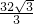米，DE=AE•1=32米，
∴CD=32米-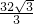米≈14米，
故选 A．
点评：本题考查了特殊角的三角函数值，考查了直角三角形中三角函数的应用，本题中求DE、CE的值是解题的关键．
分析：延长DC、交AE与E，则根据AE和∠EAC可以计算EC的长度，根据AE和∠EAD可以计算DE的长度，根据DE、CE的值即可计算CD的值，即可解题．
解答：
解：延长DC、交AE与E，∠EAC=30°，∠EAD=45°，
∴CE=AE•
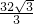=米，DE=AE•1=32米，∴CD=32米-
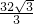米≈14米，故选 A．
点评：本题考查了特殊角的三角函数值，考查了直角三角形中三角函数的应用，本题中求DE、CE的值是解题的关键．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
如图，某大学的校门是抛物线形水泥建筑物，大门的地面宽为8m，两侧距地面4m高处各有一个挂校名横匾用的铁环，两铁环的水平距离为6m，则校门的高为
学校大门如图所示是一抛物线形水泥建筑物，大门的地面宽度为8米，两侧距地4米高处各有一挂校名横匾用的铁环，两铁环的水平距离为6米，则该校门的高度（精确到0.1米）为（ ）
