题目内容
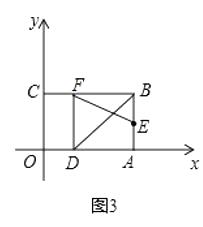
【题目】如图,正方形![]() 的边
的边![]() ,
,![]() 在坐标轴上,点
在坐标轴上,点![]() 的坐标为
的坐标为![]() .点
.点![]() 从点
从点![]() 出发,以每秒1个单位长度的速度沿
出发,以每秒1个单位长度的速度沿![]() 轴向点
轴向点![]() 运动;点
运动;点![]() 从点
从点![]() 同时出发,以相同的速度沿
同时出发,以相同的速度沿![]() 轴的正方向运动,规定点
轴的正方向运动,规定点![]() 到达点
到达点![]() 时,点
时,点![]() 也停止运动,连接
也停止运动,连接![]() ,过
,过![]() 点作
点作![]() 的垂线,与过点
的垂线,与过点![]() 平行于
平行于![]() 轴的直线
轴的直线![]() 相交于点
相交于点![]() ,
,![]() 与
与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,设点
,设点![]() 运动的时间为
运动的时间为![]() 秒.
秒.
(1)线段![]() (用含
(用含![]() 的式子表示),点
的式子表示),点![]() 的坐标为 (用含
的坐标为 (用含![]() 的式子表示),
的式子表示),![]() 的度数为 .
的度数为 .
(2)经探究![]() 周长是一个定值,不会随时间
周长是一个定值,不会随时间![]() 的变化而变化,请猜测周长的值并证明.
的变化而变化,请猜测周长的值并证明.
(3)①当![]() 为何值时,有
为何值时,有![]() .
.
②![]() 的面积能否等于
的面积能否等于![]() 周长的一半,若能求出此时
周长的一半,若能求出此时![]() 的长度;若不能,请说明理由.
的长度;若不能,请说明理由.
【答案】(1)![]() ,(t,t),45°;(2)△POE周长是一个定值为10,理由见解析;(3)①当t为(5
,(t,t),45°;(2)△POE周长是一个定值为10,理由见解析;(3)①当t为(5![]() -5)秒时,BP=BE;②能,PE的长度为2
-5)秒时,BP=BE;②能,PE的长度为2![]() .
.
【解析】
(1)由勾股定理得出BP的长度;易证△BAP≌△PQD,从而得到DQ=AP=t,从而可以求出∠PBD的度数和点D的坐标.
(2)延长OA到点F,使得AF=CE,证明△FAB≌△ECB(SAS).得出FB=EB,∠FBA=∠EBC.再证明△FBP≌△EBP(SAS).得出FP=EP.得出EP=FP=FA+AP=CE+AP.即可得出答案;
(3)①证明Rt△BAP≌Rt△BCE(HL).得出AP=CE.则PO=EO=5-t.由等腰直角三角形的性质得出PE=![]() PO=
PO=![]() (5-t).延长OA到点F,使得AF=CE,连接BF,证明△FAB≌△ECB(SAS).得出FB=EB,∠FBA=∠EBC.证明△FBP≌△EBP(SAS).得出FP=EP.得出EP=FP=FA+AP=CE+AP.得出方程
(5-t).延长OA到点F,使得AF=CE,连接BF,证明△FAB≌△ECB(SAS).得出FB=EB,∠FBA=∠EBC.证明△FBP≌△EBP(SAS).得出FP=EP.得出EP=FP=FA+AP=CE+AP.得出方程![]() (5-t)=2t.解得t=5
(5-t)=2t.解得t=5![]() -5即可;
-5即可;
②由①得:当BP=BE时,AP=CE.得出PO=EO.则△POE的面积=![]() OP2=5,解得OP=
OP2=5,解得OP=![]() ,得出PE=
,得出PE=![]() OP-
OP-![]() =2
=2![]() 即可.
即可.
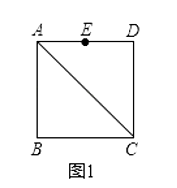
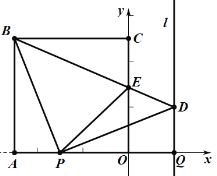
解:(1)如图1,
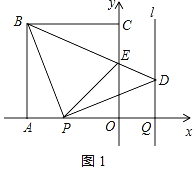
由题可得:AP=OQ=1×t=t,
∴AO=PQ.
∵四边形OABC是正方形,
∴AO=AB=BC=OC,∠BAO=∠AOC=∠OCB=∠ABC=90°.
∴BP=![]() ,
,
∵DP⊥BP,
∴∠BPD=90°.
∴∠BPA=90°-∠DPQ=∠PDQ.
∵AO=PQ,AO=AB,
∴AB=PQ.
在△BAP和△PQD中,
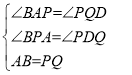 ,
,
∴△BAP≌△PQD(AAS).
∴AP=QD,BP=PD.
∵∠BPD=90°,BP=PD,
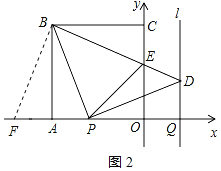
∴∠PBD=∠PDB=45°.
∵AP=t,
∴DQ=t
∴点D坐标为(t,t).
故答案为:![]() ,(t,t),45°.
,(t,t),45°.
(2)△POE周长是一个定值为10,理由如下:
延长OA到点F,使得AF=CE,连接BF,如图2所示.
在△FAB和△ECB中,
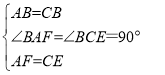 ,
,
∴△FAB≌△ECB(SAS).
∴FB=EB,∠FBA=∠EBC.
∵∠EBP=45°,∠ABC=90°,
∴∠ABP+∠EBC=45°.
∴∠FBP=∠FBA+∠ABP=∠EBC+∠ABP=45°.
∴∠FBP=∠EBP.
在△FBP和△EBP中,
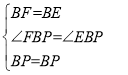 ,
,
∴△FBP≌△EBP(SAS).
∴FP=EP.
∴EP=FP=FA+AP=CE+AP.
∴OP+PE+OE=OP+AP+CE+OE=AO+CO=5+5=10.
∴△POE周长是定值,该定值为10.
(3)①若BP=BE,
在Rt△BAP和Rt△BCE中,
![]() ,
,
∴Rt△BAP≌Rt△BCE(HL).
∴AP=CE.
∵AP=t,
∴CE=t.
∴PO=EO=5-t.
∵∠POE=90°,
∴△POE是等腰直角三角形,
∴PE=![]() PO=
PO=![]() (5-t).
(5-t).
延长OA到点F,使得AF=CE,连接BF,如图2所示.
在△FAB和△ECB中,
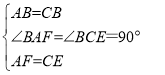 ,
,
∴△FAB≌△ECB(SAS).
∴FB=EB,∠FBA=∠EBC.
∵∠EBP=45°,∠ABC=90°,
∴∠ABP+∠EBC=45°.
∴∠FBP=∠FBA+∠ABP=∠EBC+∠ABP=45°.
∴∠FBP=∠EBP.
在△FBP和△EBP中,
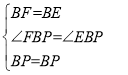 ,
,
∴△FBP≌△EBP(SAS).
∴FP=EP.
∴EP=FP=FA+AP=CE+AP.
∴EP=t+t=2t.
∴![]() (5-t)=2t.
(5-t)=2t.
解得:t=5![]() -5,
-5,
∴当t为(5![]() -5)秒时,BP=BE.
-5)秒时,BP=BE.
②△POE的面积能等于△POE周长的一半;理由如下:
由①得:当BP=BE时,AP=CE.
∵AP=t,
∴CE=t.
∴PO=EO.
则△POE的面积=![]() OP2=5,
OP2=5,
解得:OP=![]() ,
,
∴PE=![]() OP=
OP=![]() =2
=2![]() ;
;
即△POE的面积能等于△POE周长的一半,此时PE的长度为2![]() .
.

【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)根据图示填写下表;
平均数(分) | 中位数(分) | 众数(分) | |
初中部 | 85 | ||
高中部 | 85 | 100 |
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.