题目内容
在直线l上依次摆放着七个正方形(如图所示),已知斜放置的三个正方形的面积分别是1,2,3,正放置的四个正方形的面积依次是S1, S2 ,S3 ,S4 ,则S1+ S2 +S3 +S4 = .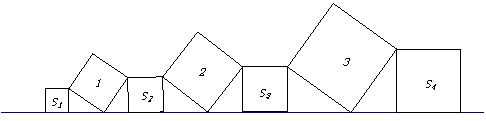
4
解析试题分析:第一个正方形和第二个正方形中间的三角形间隙与第二个正方形和第三个正方形之间的三角形间隙全等,即两个间隙之间的三角形全等,设七个正方形的边依次为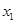 到
到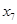 ,第二个正方形的边的平方为第一个正方形的边的平方加上两个正方形之间的最长距离,即
,第二个正方形的边的平方为第一个正方形的边的平方加上两个正方形之间的最长距离,即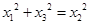 ,同理,
,同理,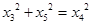 ,
,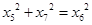 ,又
,又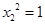 ,
,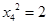 ,
,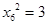 ,所以
,所以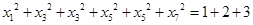 ,而
,而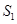
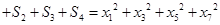 ,所以
,所以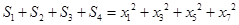
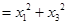
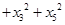
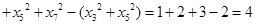
考点:勾股定理与全等三角形的结合
点评:此题关键在于看出第一个正方形与第三个正方形的边的关系,两边的平方和等于第二个正方形的边的平方

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目

 7、在直线l上依次摆放着三个正方形(如图所示).已知斜放置的正方形的面积是1,正放置的两个正方形的面积依次是s1,s2.则s1,s2,1之间的关系( )
7、在直线l上依次摆放着三个正方形(如图所示).已知斜放置的正方形的面积是1,正放置的两个正方形的面积依次是s1,s2.则s1,s2,1之间的关系( )

