题目内容
1．
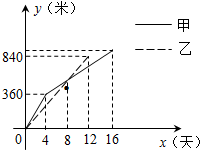我市某县在实施“村村通”工程中，决定在A、B两村之间修筑一条公路，甲、乙两个工程队分别从A、B两村同时相向开始修筑．乙队修筑了840米后，因另有任务提前离开，余下的任务由甲队单独完成，直到道路修通．两队开工8天时，所修道路的长度都为560米，甲、乙两个工程队所修道路的长度y（米）与修筑时间x（天）之间的关系图象如图所示．下列说法：①乙工程队每天修路70米；
②甲工程队后12天中每天修路50米；
③该公路全长1640米；
④若乙工程队不提前离开，则两队只需要13$\frac{2}{3}$天就能完成任务，
其中正确的结论有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
分析 根据函数图象可以判断题目中的各种说法是否正确，从而可以解答本题．
解答 解：由图象可得，
乙工程队每天修路：560÷8=70米，故①正确；
甲工程队后12天每天修路：（560-360）÷（8-4）=50米，故②正确；
该公路全长为：840+360+50×（16-4）=840+360+600=1800米，故③错误；
若乙工程队不提前离开，则两队需要的时间为：12+（1800-840×2）÷（50+70）=13天，故④错误；
故选B．
点评 本题考查一次函数的应用，解题的关键是明确题意，利用数形结合的思想解答问题．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
已知二次函数y=-$\frac{1}{2}{x^2}$-x+3．
9．用加减消元法解方程组$\left\{\begin{array}{l}{3x-2y=2}\\{x+y=5}\end{array}\right.$，下列变形正确的是（ ）
| A． | $\left\{\begin{array}{l}{3x-y=2}\\{x+2y=5}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{3x-2y=2}\\{x+2y=5}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{3x-2y=2}\\{3x+3y=15}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{3x-2y=2}\\{2x+2y=5}\end{array}\right.$ |
16．与抛物线y=-$\frac{1}{2}$x2的开口方向相同的抛物线是（ ）
| A． | $y=\frac{1}{4}{x^2}$ | B． | y=-x2-x | C． | $y=\frac{1}{2}{x^2}+10$ | D． | y=x2+2x-5 |
11．下列式子中能用公式法分解因式的是（ ）
| A． | a2+ab+b2 | B． | a2+2a+2 | C． | a2-2b+b2 | D． | a2+2a+1 |