��Ŀ����
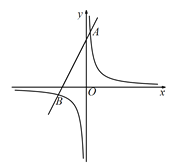
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У���![]() ��
��![]() ����
����![]() ��
��![]() �ᷭ�۵õ�
�ᷭ�۵õ�![]() ����֪������
����֪������![]() ����
����![]() ��
��![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��
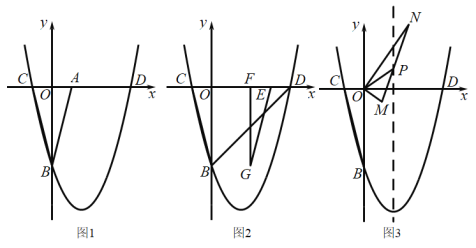
��1�������߶��������Ϊ_______��
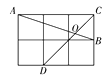
��2����ͼ2��![]() ��
��![]() ��������ÿ��
��������ÿ��![]() ����λ���ȵ��ٶ�ƽ�Ƶõ�
����λ���ȵ��ٶ�ƽ�Ƶõ�![]() ���˶�ʱ��Ϊ
���˶�ʱ��Ϊ![]() �룮��
�룮��![]() ʱ����
ʱ����![]() ��
��![]() �ص����
�ص����![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
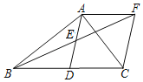
��3����ͼ3����![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת�õ�
˳ʱ����ת�õ�![]() ���߶�
���߶�![]() �������߶Գ��ύ�ڵ�
�������߶Գ��ύ�ڵ�![]() ������תһȦ�����У��Ƿ���ڵ�
������תһȦ�����У��Ƿ���ڵ�![]() ��ʹ��
��ʹ��![]() �������ڣ�ֱ��д���������������ĵ�
�������ڣ�ֱ��д���������������ĵ�![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��![]() ����2��
����2��![]() ����3�����ڣ���
����3�����ڣ���![]() ��
��![]() ����
����![]() ��
��![]() ��
��
��������
��1������Գƿɵõ�B��C���꣬����������߽���ʽ�������õ������߶������ꣻ
��2��������������������Σ���t��ʾ�����߶Σ����ø����ʾ![]() ��
��![]() �ص�������ɣ�
�ص�������ɣ�
��3���������֪����PΪ�߶�MN�е㣬�����������ʣ����P�����꣬���M��m��n�����꣬�������������ƿɵ�N�����꣬���е����깫ʽ�ɱ�ʾP�����꣬���췽�̿���m��n��������ɽ�.
�⣺��1������֪����C����Ϊ��-1,0��
�ѣ�-1,0������0��-4������![]() ����
����
![]()
��ã�![]()
��![]()
��Գ���Ϊֱ��![]()
������������![]()
�� ��������Ϊ![]()
�ʴ�Ϊ��![]()
��2����BG����BD��GE�ڵ�K��BD��FG�� T����K��HK��FG��H

�ɣ�1����֪����D����Ϊ��4,0��
��![]()
����֪��![]() ��
��
��GB��OD
��![]()
����![]() ����
����![]() ��
��
�ã�![]()
![]() ��
��
![]()
![]()
��3����![]() ��
��![]() ����
����![]() ��
��![]() ��
��
��ͼ����M�ڵ�������ʱ�����������֪������![]() ��
��![]() �е�ʱ��
�е�ʱ��![]()
��MN=BC=![]()
��![]() ��
��
P��x�������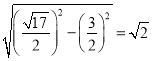
�ɵã�![]()
�ֱ����M��N��MF��y���ڵ�F��NE��y���ڵ�E
![]()
0
��![]()
��![]()
��![]()
��![]()
![]()
����![]() ����
����![]() ��
��
���P������![]() ��
��![]() ��
��
��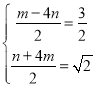
���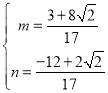
��M������![]() ��
��![]() ��
��
����M�ڵ�������ʱ��ͬ������![]() ����
����![]()
���P������![]() ��
��![]() ��
��
ͬ����![]()
��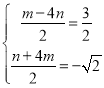
���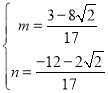
��M������![]() ��
��![]() ��
��
�ʴ�Ϊ��![]() ��
��![]() ����
����![]() ��
��![]() ��
��

 ��У����ϵ�д�
��У����ϵ�д�