题目内容
6.根据要求,解答下列问题.(1)先化简,再求值:$\frac{1}{2}$x2y-[6xy-4($\frac{3}{2}$xy-x2y)],其中x取最大负整数,y=-$\frac{6}{7}$.
(2)化简:(x3+5x2+4x-4)-(-x2+2x3-3x-1)+(3-7x-6x2+x3).
分析 (1)原式去括号合并得到最简结果,确定出x的值,把x与y的值代入计算即可求出值;
(2)原式去括号合并即可得到结果.
解答 解:(1)原式=$\frac{1}{2}$x2y-6xy+6xy-4x2y=-$\frac{7}{2}$x2y,
由x取最大负整数得x=-1,
当x=-1,y=-$\frac{6}{7}$时,原式=-$\frac{7}{2}$×1×(-$\frac{6}{7}$)=3;
(2)原式=x3+5x2+4x-4+x2-2x3+3x+1+3-7x-6x2+x3
=(1-2+1)x3+(5+1-6)x2+(4+3-7)x+(-4+1+3)
=0.
点评 此题考查了整式的加减-化简求值,熟练掌握去括号法则与合并同类项法则是解本题的关键.

练习册系列答案
相关题目
16.下列事件中,属于随机事件的是( )
| A. | 任意买一张电影票,座位号是偶数 | |
| B. | 袋中只有5只黄球,摸出一个球是白球 | |
| C. | 用长度分别是2cm,3cm,6cm的细木条首尾相连组成一个三角形 | |
| D. | 从分别写有2,4,6的三张卡片中随机抽出一张,卡片上的数字能被2整除 |
11. 图(1)是一个长为 2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是( )
图(1)是一个长为 2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是( )
 图(1)是一个长为 2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是( )
图(1)是一个长为 2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是( )| A. | a2-b2 | B. | (a-b)2 | C. | (a+b)2 | D. | ab |
15.去括号-a-(b-2)=( )
| A. | -a-b-2 | B. | a+b-2 | C. | -a-b+2 | D. | -a+b-2 |
16.下列计算结果正确的是( )
| A. | (-3)2=6 | B. | (-1)2017=-1 | C. | -2+3=-5 | D. | -|-3|=3 |
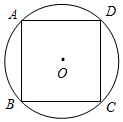 如图,正方形ABCD内接于⊙O,弦BC所对的圆周角的度数为45°或135°.
如图,正方形ABCD内接于⊙O,弦BC所对的圆周角的度数为45°或135°.