题目内容
16.在△ABC中,已知AC=2,BC=3,sinB=$\frac{2}{5}$,求sinA.分析 直接利用正弦定理即可.
解答 解:在△ABC中,AC=2,BC=3,sinB=$\frac{2}{5}$,
由正弦定理得:sinA=$\frac{a•sinB}{b}$=$\frac{3×\frac{2}{5}}{2}$=$\frac{3}{5}$.
点评 本题主要考查了正弦定理的运用,熟练掌握$\frac{a}{sinA}=\frac{b}{sinB}$是解答此题的关键.

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
4.2008年将在北京举办第29届夏季奥运会,观察下表
若用n表示奥运会届数,试用含n的代数式表示相应的举办年份是( )
| 届数 | 第1届 | 第2届 | 第3届 | … | 第29届 | … |
| 举办年份 | 1896年 | 1900年 | 1904年 | 2008年 |
| A. | 4n | B. | 4n+1892 | C. | 4n+1896 | D. | 4n+2008 |
8.实数-$\frac{1}{2}$的绝对值是( )
| A. | 2 | B. | -2 | C. | -|$\frac{1}{2}$| | D. | $\frac{1}{2}$ |
5.若反比例函数为y=$\frac{-2}{x}$,则这个函数的图象位于( )
| A. | 第一、二象限 | B. | 第一、三象限 | C. | 第二、三象限 | D. | 第二、四象限 |
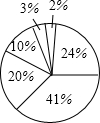 根据如图的数据制作扇形统计图并回答问题
根据如图的数据制作扇形统计图并回答问题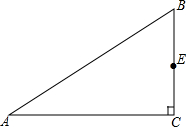 已知,如图,△ABC中,∠C=90°,E为BC边中点.
已知,如图,△ABC中,∠C=90°,E为BC边中点.