题目内容
6.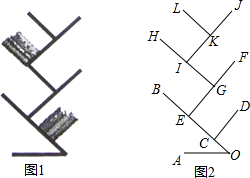 图1是小明利用废弃的钢条焊接成的创意书架,现将其结构简化成图2所示的图形,制作过程为:首先将两根钢条OA和OB焊接成∠AOB=45°,OB=70cm,BC=EF=HG=IJ=60cm,焊接点E、G、I分别为BC、EF、HG的中点,钢条KL、CD的长均为30cm,所有在点C,E,G,I,K焊接处的相邻两根钢条互相垂直.
图1是小明利用废弃的钢条焊接成的创意书架,现将其结构简化成图2所示的图形,制作过程为:首先将两根钢条OA和OB焊接成∠AOB=45°,OB=70cm,BC=EF=HG=IJ=60cm,焊接点E、G、I分别为BC、EF、HG的中点,钢条KL、CD的长均为30cm,所有在点C,E,G,I,K焊接处的相邻两根钢条互相垂直.(1)求证:L,J所在直线与直线OA平行;
(2)求书架的高度.(结果保留一位小数,$\sqrt{2}≈1.414$)
分析 (1)连接ED,先求得∠CED=45°,根据内错角相等求得OA∥ED,同理BG∥ED,IF∥BG,HK∥IF,LJ∥HK,即可证得L,J所在直线与直线OA平行;
(2)延长JI交直线OA于点M,根据已知求得∠HIJ=∠HGF=∠BEF=90°,求得JM∥EF,进而求得,∠M=45°,BM=OB=70cm,JB=90cm,进而得出JM=160cm,然后通过解正弦函数即可求得书架的高度.
解答  解:(1)连接ED,
解:(1)连接ED,
∵焊接点E为BC的中点,BC=60cm,
∴EC=CD=30cm,
∵CD⊥EC,
∴∠CED=45°,
∴∠AOB=∠CED,OA∥ED,
同理BG∥ED,IF∥BG,HK∥IF,LJ∥HK,
∴LJ∥OA;
(2)延长JI交直线OA于点M,
∵所有在点C,E,G,I,K焊接处的相邻两根钢条互相垂直,
∴∠HIJ=∠HGF=∠BEF=90°,
∴JM∥EF,
∵BE=IG=IK=KJ=30cm,
∴JM过点B,∠M=45°,BM=OB=70cm,JB=90cm,
∴JM=160cm,
∴书架的高度为:JM•sin45°=80$\sqrt{2}$≈113.1(cm).
点评 本题考查了平行线的判定和性质,解直角三角函数,把实际问题转化成为解直角三角形的问题是解题的关键.

练习册系列答案
相关题目
1.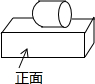 如图是由一个圆柱和长方体组合而成的几何体,它的俯视图是( )
如图是由一个圆柱和长方体组合而成的几何体,它的俯视图是( )
 如图是由一个圆柱和长方体组合而成的几何体,它的俯视图是( )
如图是由一个圆柱和长方体组合而成的几何体,它的俯视图是( )| A. | 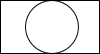 | B. | 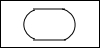 | C. |  | D. |  |
11.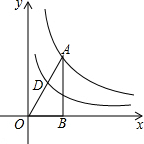 如图,反比例函数y=$\frac{8}{x}$的图象经过直角三角形OAB的顶点A,D为斜边OA的中点,则过点D的反比例函数的解析式是( )
如图,反比例函数y=$\frac{8}{x}$的图象经过直角三角形OAB的顶点A,D为斜边OA的中点,则过点D的反比例函数的解析式是( )
 如图,反比例函数y=$\frac{8}{x}$的图象经过直角三角形OAB的顶点A,D为斜边OA的中点,则过点D的反比例函数的解析式是( )
如图,反比例函数y=$\frac{8}{x}$的图象经过直角三角形OAB的顶点A,D为斜边OA的中点,则过点D的反比例函数的解析式是( )| A. | y=$\frac{6}{x}$ | B. | y=-$\frac{4}{x}$ | C. | y=$\frac{2}{x}$ | D. | y=$\frac{1}{x}$ |
18. 如图,AB是⊙O的直径,点A是弧CD的中点,若∠B=25°,则∠AOC=( )
如图,AB是⊙O的直径,点A是弧CD的中点,若∠B=25°,则∠AOC=( )
 如图,AB是⊙O的直径,点A是弧CD的中点,若∠B=25°,则∠AOC=( )
如图,AB是⊙O的直径,点A是弧CD的中点,若∠B=25°,则∠AOC=( )| A. | 25° | B. | 30° | C. | 40° | D. | 50° |
15. 用图中两个可自由转动的转盘做“配紫色”游戏:分别旋转两个转盘,若其中一个转出红色,另一个转出蓝色即可配成紫色,那么可配成紫色的概率是( )
用图中两个可自由转动的转盘做“配紫色”游戏:分别旋转两个转盘,若其中一个转出红色,另一个转出蓝色即可配成紫色,那么可配成紫色的概率是( )
 用图中两个可自由转动的转盘做“配紫色”游戏:分别旋转两个转盘,若其中一个转出红色,另一个转出蓝色即可配成紫色,那么可配成紫色的概率是( )
用图中两个可自由转动的转盘做“配紫色”游戏:分别旋转两个转盘,若其中一个转出红色,另一个转出蓝色即可配成紫色,那么可配成紫色的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{3}{4}$ |
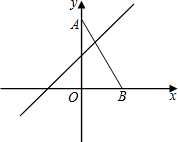 已知平面直角坐标系中,O为坐标原点,点A坐标为(0,8),点B坐标为(4,0),点E是直线y=x+4上的一个动点,若∠EAB=∠ABO,则点E的坐标为(4,8)或(-12,-8).
已知平面直角坐标系中,O为坐标原点,点A坐标为(0,8),点B坐标为(4,0),点E是直线y=x+4上的一个动点,若∠EAB=∠ABO,则点E的坐标为(4,8)或(-12,-8). 如图,平面上直线a,b分别经过线段OK两端点(数据如图),则a,b相交所成的锐角是30°.
如图,平面上直线a,b分别经过线段OK两端点(数据如图),则a,b相交所成的锐角是30°.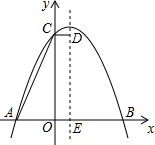 如图,抛物线y=ax2+bx+c与x轴交于A、B两点,其中B点坐标为(4,0),直线DE是抛物线的对称轴,且与x轴交于点E,CD⊥DE于D,则下列结论正确的序号为①③④(多填或错填得0分,少填酌情给分)
如图,抛物线y=ax2+bx+c与x轴交于A、B两点,其中B点坐标为(4,0),直线DE是抛物线的对称轴,且与x轴交于点E,CD⊥DE于D,则下列结论正确的序号为①③④(多填或错填得0分,少填酌情给分) 如图,已知点A1,A2,…,An均在直线y=x-1上,点B1,B2,…,Bn均在双曲线y=-$\frac{1}{x}$上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-1,则a2015=2.
如图,已知点A1,A2,…,An均在直线y=x-1上,点B1,B2,…,Bn均在双曲线y=-$\frac{1}{x}$上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-1,则a2015=2.