题目内容
6.一个直角三角形的两条直角边长是方程x2-7x+12=0的两个根,则此直角三角形的内切圆的半径为1.分析 先解一元二次方程,根据勾股定理解得三角形的斜边,利用直角三角形内切圆的半径等于两直角边之和与斜边之差的一半,可得结果.
解答 解:解方程x2-7x+12=0得,
x1=3,x2=4,
由勾股定理得,斜边为5,
∴此直角三角形的内切圆的半径为=$\frac{1}{2}×(3+4-5)$=1,
故答案为:1.
点评 本题主要考查了因式分解法解一元二次方程,熟记直角三角形内切圆的半径等于两直角边之和与斜边之差的一半是解答此题的关键.

练习册系列答案
相关题目
16.平行四边形不一定具有的特征是( )
| A. | 两组对边分别平行 | B. | 两组对角分别相等 | ||
| C. | 对角线相等 | D. | 内角和为360° |
17.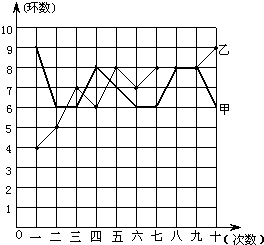 射击集训队在在一个月的集训中,对甲、乙两名运动员进行了10次测试,成绩如图所示(折线图中,粗线表示甲,细线表示乙):
射击集训队在在一个月的集训中,对甲、乙两名运动员进行了10次测试,成绩如图所示(折线图中,粗线表示甲,细线表示乙):
(1)根据如图所提供的信息填写表格;
(2)如果你是教练,会选择哪位运动员参加比赛?请结合表中三个统计指标以及折线统计图说明理由.
 射击集训队在在一个月的集训中,对甲、乙两名运动员进行了10次测试,成绩如图所示(折线图中,粗线表示甲,细线表示乙):
射击集训队在在一个月的集训中,对甲、乙两名运动员进行了10次测试,成绩如图所示(折线图中,粗线表示甲,细线表示乙):(1)根据如图所提供的信息填写表格;
| 平均数 | 极差 | 方差 | |
| 甲 | 7 | 3 | 1.2 |
| 乙 | 7 | 5 | 2.2 |
14.下列说法正确的是( )
| A. | 有公共顶点的两个角是对顶角 | B. | 相等的角是对顶角 | ||
| C. | 有公共顶点且相等的角是对顶角 | D. | 对顶角相等 |
18.已知双曲线y=$\frac{a}{x}$与直线y=kx在第一象限的交点为A (3,5),则双曲线y=$\frac{a}{x}$与直线y=kx另一个交点B的坐标为( )
| A. | (-3,5) | B. | (3,-5) | C. | (-5,-3) | D. | (-3,-5) |
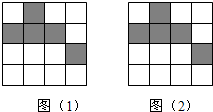 如图(1)、(2)分别是由16个小正方形组成的正方形网格图,现已将其中部分小正方形涂黑,请你用两种不同的方法,分别在两个图中再涂黑两个空白的小正方形,使它(涂黑部分)成为轴对称图形.
如图(1)、(2)分别是由16个小正方形组成的正方形网格图,现已将其中部分小正方形涂黑,请你用两种不同的方法,分别在两个图中再涂黑两个空白的小正方形,使它(涂黑部分)成为轴对称图形. 如图,已知函数y1=3x+b和y2=ax-3的图象交于点P(-2,-5),则不等式3x+b>ax-3的解集为x>-2.
如图,已知函数y1=3x+b和y2=ax-3的图象交于点P(-2,-5),则不等式3x+b>ax-3的解集为x>-2.