题目内容
 有一块三角形纸板(如图)AC=60cm,BC=80cm,AB=100cm,小华想用它剪一个正方形,使正方形的每个顶点都在三角形的边上,请你帮她计算剪下的正方形的边长.
有一块三角形纸板(如图)AC=60cm,BC=80cm,AB=100cm,小华想用它剪一个正方形,使正方形的每个顶点都在三角形的边上,请你帮她计算剪下的正方形的边长.
 解:∵△ABC中,AC=60cm,BC=80cm,AB=100cm,
解:∵△ABC中,AC=60cm,BC=80cm,AB=100cm,∴AC2+BC2=AB2,
∴∠C=90°
∴CN=
 =48
=48∵四边形DEFG是正方形,
∴GD∥BA,DG=EF,
∴△CDG∽△CAB,
又∵CN⊥BA,
∴AN⊥DG,DG=ED=EF,
∴
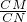 =
= ,
,设DE=x,则CM=48-x,
∴
 =
= ,
,解得:x=
 .
.答:这个正方形的边长为
 厘米.
厘米.分析:首先利用三角形的性质和勾股定理求得AB边上的高CN,然后利用相似三角形的性质求得线段MN即为正方形的边长.
点评:本题考查相似三角形性质的应用.解题时关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
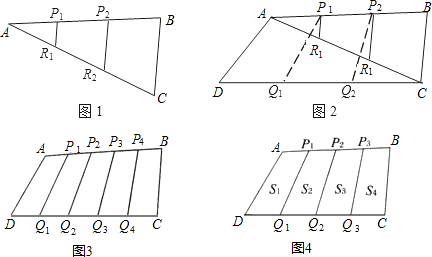

 =
= S△ABC,请证明;
S△ABC,请证明; 与S四边形ABCD之间的数量关系;
与S四边形ABCD之间的数量关系; ;
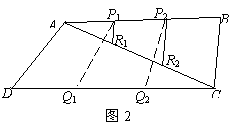
;



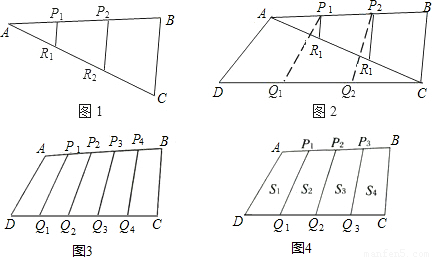
 =
= S△ABC,请证明.
S△ABC,请证明. 与S四边形ABCD之间的数量关系.
与S四边形ABCD之间的数量关系.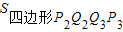 .
.