题目内容
方程a2-b2=2004的正整数解有________组.
2
分析:根据方程a2-b2=2004的正整数,则可确定a+b,a-b也为正整数解.将2004分解成正整数的相乘的形式.因而可分解为2×1002、3×668、4×501、6×334、12×167这五种.再就这五种情况分别求出a、b的值,验证是否是正整数.
解答:∵方程a2-b2=2004的解是正整数,
∴a+b,a-b也为正整数,即(a+b)(a-b)=2004,
又∵2004可分解为2与1002、3与668、4与501、6与334、12与167,
①当2004分解为2与1002时,则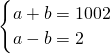 ,解得a=504,b=502,符号题意;
,解得a=504,b=502,符号题意;
②当2004分解为3与668时,则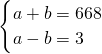 ,解得a=
,解得a=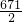 ,b=
,b=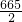 ,与正整数解矛盾,故舍去;
,与正整数解矛盾,故舍去;
③当2004分解为4与501时,则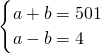 ,解得a=
,解得a=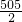 ,b=
,b=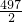 ,与正整数解矛盾,故舍去;
,与正整数解矛盾,故舍去;
④当2004分,6与334时,则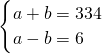 ,解得a=170,b=164,符号题意;
,解得a=170,b=164,符号题意;
⑤当2004分解,12与167时,则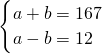 ,解得a=
,解得a= ,b=
,b=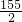 ,与正整数解矛盾,故舍去.
,与正整数解矛盾,故舍去.
故答案为2.
点评:本题考查因式分解.解决本题的关键是将2004写成两个正整数相乘的形式、a2-b2写成(a+b)(a-b)的形式,并与前者对应相等,求解a、b.
分析:根据方程a2-b2=2004的正整数,则可确定a+b,a-b也为正整数解.将2004分解成正整数的相乘的形式.因而可分解为2×1002、3×668、4×501、6×334、12×167这五种.再就这五种情况分别求出a、b的值,验证是否是正整数.
解答:∵方程a2-b2=2004的解是正整数,
∴a+b,a-b也为正整数,即(a+b)(a-b)=2004,
又∵2004可分解为2与1002、3与668、4与501、6与334、12与167,
①当2004分解为2与1002时,则
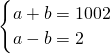 ,解得a=504,b=502,符号题意;
,解得a=504,b=502,符号题意;②当2004分解为3与668时,则
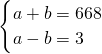 ,解得a=
,解得a=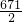 ,b=
,b=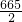 ,与正整数解矛盾,故舍去;
,与正整数解矛盾,故舍去;③当2004分解为4与501时,则
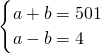 ,解得a=
,解得a=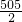 ,b=
,b=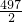 ,与正整数解矛盾,故舍去;
,与正整数解矛盾,故舍去;④当2004分,6与334时,则
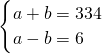 ,解得a=170,b=164,符号题意;
,解得a=170,b=164,符号题意;⑤当2004分解,12与167时,则
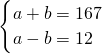 ,解得a=
,解得a= ,b=
,b=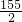 ,与正整数解矛盾,故舍去.
,与正整数解矛盾,故舍去.故答案为2.
点评:本题考查因式分解.解决本题的关键是将2004写成两个正整数相乘的形式、a2-b2写成(a+b)(a-b)的形式,并与前者对应相等,求解a、b.

练习册系列答案
相关题目