题目内容
若正整数a、b、c满足方程a2+b2=c2 ,则称这一组正整数（a、b、c）为“商高数”，下面列举五组“商高数”：（3，4，5），（5，12，13），（6，8，10），（7，24，25），（12，16，20），注意这五组“商高数”的结构有如下规律：
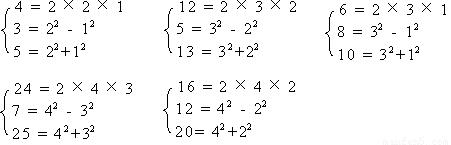
根据以上规律，回答以下问题：
（1）商高数的三个数中，有几个偶数，几个奇数？
（2）写出各数都大于30的两组商高数。
（3）用两个正整数m、n（m＞n）表示一组商高数，并证明你的结论。
【答案】
（1）有一个偶数、两个奇数或三个偶数（2）（40，42，58，），（119，120，169）（3）a = 2mn, b = m2 – n2, c = m2 + n2，证明见解析
【解析】（1）有一个偶数、两个奇数或三个偶数。（3分）
（2）（40，42，58，），（119，120，169）（3分）
（3）a = 2mn, b = m2 – n2, c = m2 + n2
证明：a2 +b2 = (2 m n)2+ ( m2 – n2)2
= 4m2n2 +m4 -2m2n2
4
= m4 +2m2n2+n4 = (m2+n2 )2
∴ a2+b2 = c2（4分）
（1）根据奇数和偶数的定义解答；
（2）根据a=2mn，b=m2-n2，c=m2+n2找出符合条件的两组数据；
（3）根据勾股定理证明这一组数据是商高数．
练习册系列答案
相关题目
22、全球的环境污染日趋严重，为了使学生了解环保知识，增强环保意识，某中学举行了有900名学生参加的“环保知识竞赛”．为了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分取正整数，满分为100分）进行统计，并制作成图表如下：
青少年“心理健康”问题已引起了社会的关注，希望中学对全校600名学生进行了一次“心理健康”只是测试，并从中抽取了部分学生的成绩（
得分取正整数，满分为100分）作为样本，绘制了下面尚未完成的频率分布表和频率分布直方图．
请回答下列问题：
（1）填写频率分布表中的空格，并补全频率分布直方图；
（2）在频率分布直方图中，梯形ABCD的面积是多少？
（3）若成绩在90分以上（不含90分）为优秀，试估计该校成绩优秀的有多少人？
（4）能否确定测试成绩的众数落在那个分组内？
得分取正整数，满分为100分）作为样本，绘制了下面尚未完成的频率分布表和频率分布直方图．| 分组 | 频数 | 频率 |
| 50.5～60.5 | 2 | 0.04 |
| 60.5～70.5 | 8 | 0.16 |
| 70.5～80.5 | 10 | |
| 80.5～90.5 | ||
| 90.5～100.5 | 14 | 0.28 |
| 合计 | 1.00 |
（1）填写频率分布表中的空格，并补全频率分布直方图；
（2）在频率分布直方图中，梯形ABCD的面积是多少？
（3）若成绩在90分以上（不含90分）为优秀，试估计该校成绩优秀的有多少人？
（4）能否确定测试成绩的众数落在那个分组内？
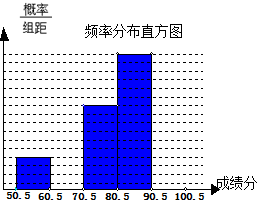22、为了让学生了解环保知识，增强环保意识，某中学举行了一次“环保知识竞赛”，共有900名学生参加了这次竞赛，为了解本次竞赛成绩情况，从中抽取了50名学生的成绩（得分取正整数，满分为100分）进行统计，请你根据下面尚未完成的频数分布表和频数分布直方图，解答下列问题：
21、某校300名初二年级学生进行数学测验，从中随机抽取部分学生的成绩（得分取正整数，满分为100分）进行统计，请你根据下面尚未完成并有局部污染的频率分布表和频率分布直方图（如图）．回答下列问题．