题目内容
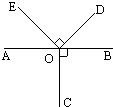16、如图，O是直线AB上一点，OC⊥AB，OE⊥OD，若∠AOE=55°，∠DOC=125°
．分析：根据已知条件“OE⊥OD”和观察图形可知∠BOD与∠EOA互余，∠DOC=∠DOB+∠COB．
解答：解：∵OE⊥OD，
∴∠EOD=90°；
∵∠AOE=55°
∴∠DOB=90°-∠AOE=90°-55°=35°；
又∵OC⊥AB，
∴∠COB=90°，
∴∠DOC=∠DOB+∠COB=90°+35°=125°．
故答案是：125°．
∴∠EOD=90°；
∵∠AOE=55°
∴∠DOB=90°-∠AOE=90°-55°=35°；
又∵OC⊥AB，
∴∠COB=90°，
∴∠DOC=∠DOB+∠COB=90°+35°=125°．
故答案是：125°．
点评：本题利用垂直的定义．解题时，要注意领会由垂直得直角这一要点．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
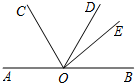如图，O是直线AB上一点，OC，OD，OE是三条射线，且OC平分∠AOD，∠BOE=2∠DOE，∠COE=80°，求∠BOE的度数．
如图，O是直线AB上一点，∠AOC=134°18′，求∠BOC的度数．
如图，O是直线AB上的一点，∠AOC=53°17′，则∠BOC的度数是
如图，O是直线AB上任意一点，OC平分∠AOB．按下列要求画图并回答问题：