题目内容
17.已知矩形的两堆角线所夹的角为60°,且其中一条对角线长为4cm,则该矩形较长的边长度是2$\sqrt{3}$cm.分析 矩形的两对角线所夹的角为60°,加上矩形的性质可得到△AOB的形状为等边三角形,进而根据已知线段AC,求得对角线的一半长,那么可得到AB长,根据勾股定理可得到BC长.
解答 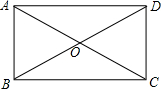 解:如图:∵四边形为矩形,∠DOC=60°,BD=AC=4cm,
解:如图:∵四边形为矩形,∠DOC=60°,BD=AC=4cm,
∴OD=OC=$\frac{1}{2}$AC=$\frac{1}{2}$×4=2(cm),
又∵∠DOC=60°,
∴△DOC是等边三角形,CD=OD=2cm,
在直角△DBC中,BD=4cm,CD=2cm,根据勾股定理BC=$\sqrt{B{D}^{2}-C{D}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$(cm),
故答案为:2$\sqrt{3}$cm.
点评 综合考查了矩形的性质及勾股定理的运用.矩形的两对角线所夹的角为60°,那么对角线的一边和两条对角线的一半组成等边三角形.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
12.等腰三角形的顶角是80°,它的底角是( )
| A. | 80° | B. | 50° | C. | 100° | D. | 40° |
2.已知10x=9,10y=4,则102x-3y的值为( )
| A. | 15 | B. | $\frac{81}{64}$ | C. | $\frac{64}{81}$ | D. | 以上答案都不对 |
7.抛物线y=-2(x+3)2+1对称轴是( )
| A. | 直线x=3 | B. | 直线x=1 | C. | 直线x=-1 | D. | 直线x=-3 |