题目内容
记第一个数为a1,记第二个数为a2,…,第n个数为an.若a1=32-12,a2=52-32,a3=72-52….
(1)根据你所发现的规律,用含n的式子表示an (n为大于0的自然数);
(2)先化简an,并用文字语言表述你发现的结论;
(3)两个数1000、2010是否在an中?如在,请指出是第几个数.
解:(1)∵a1=32-12,a2=52-32,a3=72-52,
∴an=(2n+1)2-(2n-1)2;
(2)an=(2n+1)2-(2n-1)2=(2n+1+2n-1)(2n+1-2n+1)=8n,
结论:第n个数an的值是n的8倍;
(3)∵1000÷8=125,
∴1000是第125个数.
∵2010÷8=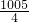 ,
,
∴2010是不在an中.
分析:(1)首先观察a1=32-12,a2=52-32,a3=72-52,即可求得an=(2n+1)2-(2n-1)2;
(2)利用平方差公式即可求得an=8n,即第n个数an的值是n的8倍;
(3)分别将1000、2010除以8,即可判定两个数1000、2010是否在an中.
点评:此题考查了数字的规律性问题,解题的关键是找到规律:an=(2n+1)2-(2n-1)2.
∴an=(2n+1)2-(2n-1)2;
(2)an=(2n+1)2-(2n-1)2=(2n+1+2n-1)(2n+1-2n+1)=8n,
结论:第n个数an的值是n的8倍;
(3)∵1000÷8=125,
∴1000是第125个数.
∵2010÷8=
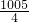 ,
,∴2010是不在an中.
分析:(1)首先观察a1=32-12,a2=52-32,a3=72-52,即可求得an=(2n+1)2-(2n-1)2;
(2)利用平方差公式即可求得an=8n,即第n个数an的值是n的8倍;
(3)分别将1000、2010除以8,即可判定两个数1000、2010是否在an中.
点评:此题考查了数字的规律性问题,解题的关键是找到规律:an=(2n+1)2-(2n-1)2.

练习册系列答案
相关题目