题目内容
如图,在正方形ABCD中,点E、F分别是BC、CD的中点,DE交AF于点M,点N为DE的中点.
(1)若AB=4,求△DNF的周长及sin∠DAF的值;
(2)求证:2AD•NF=DE•DM.
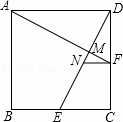
| (1)解:∵点E、F分别是BC、CD的中点, ∴EC=DF=×4=2, 由勾股定理得,DE= ∵点F是CD的中点,点N为DE的中点, ∴DN=DE=×2 NF=EC=×2=1, ∴△DNF的周长=1+ 在Rt△ADF中,由勾股定理得,AF= 所以,sin∠DAF= (2)证明:在△ADF和△DCE中,
∴△ADF≌△DCE(SAS), ∴AF=DE,∠DAF=∠CDE, ∵∠DAF+∠AFD=90°, ∴∠CDE+∠AFD=90°, ∴AF⊥DE, ∵点E、F分别是BC、CD的中点, ∴NF是△CDE的中位线, ∴DF=EC=2NF, ∵cos∠DAF= cos∠CDE= ∴ ∴2AD•NF=DE•DM. |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在平面直角坐标系中,将抛物线y=3x2先向右平移1个单位,再向上平移2个单位,得到的抛物线的解析式是( )
|
| A. | y=3(x+1)2+2 | B. | y=3(x+1)2﹣2 | C. | y=3(x﹣1)2+2 | D. | y=3(x﹣1)2﹣2 |
如图放置的几何体的左视图是( )

|
| A. |
| B. |
| C. |
| D. |
|
在下列四个立体图形中,俯视图为正方形的是( )
|
| A. |
| B. |
| C. |
| D. |
|
 =2
=2 ,
, ;
; =
= =2
=2 =
= =
= ;
; ,
, =
= ,
, =
= ,
, 已知二元一次方程组
已知二元一次方程组 的解
的解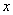 、
、 均
均 是正数,
是正数, 的取值范围。
的取值范围。 。
。 ÷(a+
÷(a+ )的值.
)的值.



 中,自变量x的取值范围是
中,自变量x的取值范围是