题目内容
如图，线段AB=8，点C是AB上一点，点D、E是线段AC的三等分点，分别以AD、DE、EC、CB为边作正方形，则AC=________时，四个正方形的面积之和最小．
6
分析：设AC为未知数，用二次函数表示出三个正方形的面积和，根据二次函数的最值问题的求法可得AC的值．
解答：设AC为x，三个正方形的面积和为y．则BC=8-x，AD=DE=EC=
，
∴y=3×（）2+（8-x）2=
x2-16x+64=，
∴x=-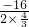
=6时，四个正方形的面积之和最小．
故答案为6．
点评：本题考查了二次函数的最值．求二次函数的最大（小）值有三种方法，第一种可由图象直接得出，第二种是配方法，第三种是公式法．
分析：设AC为未知数，用二次函数表示出三个正方形的面积和，根据二次函数的最值问题的求法可得AC的值．
解答：设AC为x，三个正方形的面积和为y．则BC=8-x，AD=DE=EC=
，∴y=3×（
）2+（8-x）2=x2-16x+64=，∴x=-
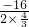=6时，四个正方形的面积之和最小．故答案为6．
点评：本题考查了二次函数的最值．求二次函数的最大（小）值有三种方法，第一种可由图象直接得出，第二种是配方法，第三种是公式法．
练习册系列答案
相关题目
21、如图，线段AB经过圆心O，交⊙O于点A，C，点D在⊙O上，连接AD，BD，∠A=∠B=30度．BD是⊙O的切线吗？请说明理由．
（2013•呼伦贝尔）如图，线段AB、DC分别表示甲乙两座建筑物的高，AB⊥BC，DC⊥BC，两建筑物的水平距离BC为30米，若甲建筑物的高AB=28米，在点A处观察乙建筑物顶部D的仰角为60°，求乙建筑物的高度 （结果保留1位小数，
如图，线段AB长为2米，AB⊥MN，垂足为A，一动点P从点A出发，以1米/秒的速度向射线AM方向移动．设移动的时间为x（秒）．
如图，线段AB上有5个点C，D，E，F，G，则图中线段的条数有（ ）