题目内容
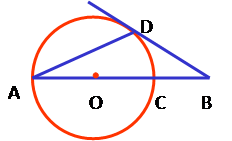
 21、如图,线段AB经过圆心O,交⊙O于点A,C,点D在⊙O上,连接AD,BD,∠A=∠B=30度.BD是⊙O的切线吗?请说明理由.
21、如图,线段AB经过圆心O,交⊙O于点A,C,点D在⊙O上,连接AD,BD,∠A=∠B=30度.BD是⊙O的切线吗?请说明理由.分析:可以先猜想BD是⊙O的切线,根据切线的判定进行分析,得到OD是圆的半径,且OD⊥BD,从而可得到结论.
解答: 解:BD是⊙O的切线.(2分)
解:BD是⊙O的切线.(2分)
连接OD;
∵OA=OD,
∴=∠ADO=∠A=30°,(4分)
∵∠A=∠B=30°,
∴∠BDA=180°-(∠A+∠B)=120°,(7分)
∴∠BDO=∠BDA-∠ADO=90°,
即OD⊥BD,
∴BD是⊙O的切线.(9分)
理由1:连接OD,∵OA=OD,
∴∠ADO=∠A=30°,(4分)
∵∠A=∠B=30°,
∴∠BDA=180°-(∠A+∠B)=120,(7分)
∴∠BDO=∠BDA-∠ADO=90°,即OD⊥BD.
∴BD是⊙O的切线.(9分)
理由2:连接OD,
∵OA=OD,
∴∠ADO=∠A=30°,(4分)
∴∠BOD=∠ADO+A=60°,(7分)
∵∠B=30°,
∴∠BDO=180°-(∠BOD+∠B)=90°,
即OD⊥BD,
∴BD是⊙O的切线.
 (9分)
(9分)
理由3:连接OD,∵OA=OD,
∴∠ADO=∠A=30°,(4分)
在BD的延长线上取一点E,
∵∠A=∠B=30°,
∴∠ADE=∠A+∠B=60°,(7分)
∴∠EDO=∠ADO+∠ADE=90°,即OD⊥BD
∴BD是⊙O的切线.(9分)
理由4:连接OD,∵OA=OD,
∴∠ADO=∠A=30°,(4分)
连接CD,则∠ADC=90°,(5分)
∴∠ODC=∠ADC-∠ADO=60°,(6分)
∵OD=OC,
∴∠OCD=60°,
∵∠B=30°,
∴∠BDC=∠OCD-∠B=30°,(7分)
∴∠ODB=∠ODC+∠BDC=90°,
即OD⊥BD,
∴BD是⊙O的切线.(9分)
 解:BD是⊙O的切线.(2分)
解:BD是⊙O的切线.(2分)连接OD;
∵OA=OD,
∴=∠ADO=∠A=30°,(4分)
∵∠A=∠B=30°,
∴∠BDA=180°-(∠A+∠B)=120°,(7分)
∴∠BDO=∠BDA-∠ADO=90°,
即OD⊥BD,
∴BD是⊙O的切线.(9分)
理由1:连接OD,∵OA=OD,
∴∠ADO=∠A=30°,(4分)
∵∠A=∠B=30°,
∴∠BDA=180°-(∠A+∠B)=120,(7分)
∴∠BDO=∠BDA-∠ADO=90°,即OD⊥BD.
∴BD是⊙O的切线.(9分)
理由2:连接OD,
∵OA=OD,
∴∠ADO=∠A=30°,(4分)
∴∠BOD=∠ADO+A=60°,(7分)
∵∠B=30°,
∴∠BDO=180°-(∠BOD+∠B)=90°,
即OD⊥BD,
∴BD是⊙O的切线.
 (9分)
(9分)理由3:连接OD,∵OA=OD,
∴∠ADO=∠A=30°,(4分)
在BD的延长线上取一点E,
∵∠A=∠B=30°,
∴∠ADE=∠A+∠B=60°,(7分)
∴∠EDO=∠ADO+∠ADE=90°,即OD⊥BD
∴BD是⊙O的切线.(9分)
理由4:连接OD,∵OA=OD,
∴∠ADO=∠A=30°,(4分)
连接CD,则∠ADC=90°,(5分)
∴∠ODC=∠ADC-∠ADO=60°,(6分)
∵OD=OC,
∴∠OCD=60°,
∵∠B=30°,
∴∠BDC=∠OCD-∠B=30°,(7分)
∴∠ODB=∠ODC+∠BDC=90°,
即OD⊥BD,
∴BD是⊙O的切线.(9分)
点评:本题考查切线的判定方法及圆周角定理的综合运用.

练习册系列答案
相关题目
 22、如图,线段AB经过圆心O,交⊙O于点A、C,∠BAD=∠B=30°,边BD交圆于点D,求证BD是⊙O的切线.
22、如图,线段AB经过圆心O,交⊙O于点A、C,∠BAD=∠B=30°,边BD交圆于点D,求证BD是⊙O的切线. 如图,线段AB经过圆心O,交⊙O于点A、C,BD是⊙O的切线.∠BAD=30°,边BD交圆于点D,求∠B.
如图,线段AB经过圆心O,交⊙O于点A、C,BD是⊙O的切线.∠BAD=30°,边BD交圆于点D,求∠B. 如图,线段AB经过圆心O,交⊙O于点A,C,点D在⊙O上,连接AD,BD,∠A=∠B=30°,圆的半径R.
如图,线段AB经过圆心O,交⊙O于点A,C,点D在⊙O上,连接AD,BD,∠A=∠B=30°,圆的半径R. 如图,线段AB经过圆心O,交⊙O于点A、C,∠BAD=∠B=30°,边BD交圆于点D.
如图,线段AB经过圆心O,交⊙O于点A、C,∠BAD=∠B=30°,边BD交圆于点D.