题目内容
圆外切等腰梯形的中位线等于8,则一腰长等于( )
| A、4 | B、6 | C、8 | D、10 |
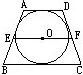
分析:如图,设圆的外切梯形ABCD,切点分别为E、H、N、中位线为MN,根据中位线定理可以得到上下底之和,然后利用切线长定理可以得到一腰长等于中位线,由此即可就问题.
解答: 解:如图,设圆的外切梯形ABCD,切点分别为E、H、N、中位线为MN,
解:如图,设圆的外切梯形ABCD,切点分别为E、H、N、中位线为MN,
∴MN=
(AB+CD),
根据切线长定理得:
DE=DH,CF=CH,并且等腰梯形和圆都是轴对称图形,
∴CD=DH+CH=DE+CF=
(AB+CD),
∴CD=MN,而MN=8,
∴CD=8.
故选C.
 解:如图,设圆的外切梯形ABCD,切点分别为E、H、N、中位线为MN,
解:如图,设圆的外切梯形ABCD,切点分别为E、H、N、中位线为MN,∴MN=
| 1 |
| 2 |
根据切线长定理得:
DE=DH,CF=CH,并且等腰梯形和圆都是轴对称图形,
∴CD=DH+CH=DE+CF=
| 1 |
| 2 |
∴CD=MN,而MN=8,
∴CD=8.
故选C.
点评:此题分别考查了切线长定理、等腰梯形的性质及梯形中位线定理,有一定的综合性,要求学生熟练掌握这些基础知识才能很好解决问题.

练习册系列答案
相关题目