题目内容

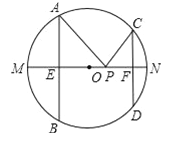
【题目】如图，AB、CD是半径为5的⊙O的两条弦，AB=8，CD=6，MN是直径，AB⊥MN于点E，CD⊥MN于点F，P为EF上的任意一点，则PA+PC的最小值为______．

【答案】

【解析】

由于A、B两点关于MN对称，因而PA+PC=PB+PC，即当B、C、P在一条直线上时，PA+PC的最小，即BC的值就是PA+PC的最小值.

解：连接OA，OB，OC，作CH垂直于AB于H．

∵AB=8，CD=6，MN是直径，AB⊥MN于点E，CD⊥MN于点F，
∴BE=AB=4，CF=CD=3，
∴OE===3,

OF===4,

∴CH=OE+OF=3+4=7，
BH=BE+EH=BE+CF=4+3=7，

在Rt△BCH中根据勾股定理得到BC===.

故答案为：.

练习册系列答案
相关题目

【题目】如图，在Rt△ABM和Rt△ADN的斜边分别为正方形的边AB和AD，其中AM=AN.

(1)求证：Rt△ABM≌Rt△AND

(2)线段MN与线段AD相交于T，若AT=,求的值

【题目】抛物线y=ax2+bx+3（a≠0）过A（4，4），B（2，m）两点，点B到抛物线对称轴的距离记为d，满足0＜d≤1，则实数m的取值范围是（　　）

A. m≤2或m≥3 B. m≤3或m≥4 C. 2＜m＜3 D. 3＜m＜4

【题目】如图，抛物线y=ax2+bx+c（a，b，c是常数，a≠0）与x轴交于A，B两点，顶点P（m，n）．给出下列结论：①2a+c＜0；②若（﹣，y1），（﹣，y2），（，y3）在抛物线上，则y1＞y2＞y3；③关于x的方程ax2+bx+k=0有实数解，则k＞c﹣n；④当n=﹣ 时，△ABP为等腰直角三角形．其中正确结论是________（填写序号）．

【题目】已知四边形ABCD中，E，F分别是AB，AD边上的点，DE与CF交于点G．

（1）如图1，若四边形ABCD是矩形，且DE⊥CF．证明:=；

（2）如图2，若四边形ABCD是平行四边形，试探究：

当∠B与∠EGC满足什么关系时，使得=成立？并证明你的结论；

（3）如图3，若BA=BC= 3，DA=DC= 4，∠BAD= 90°，DE⊥CF．求的值．

【题目】如图，OA、OB、OC都是⊙O的半径，∠AOB=2∠BOC，

（1）求证：∠ACB=2∠BAC；

（2）若AC平分∠OAB，求∠AOC的度数．

【题目】一个不透明的袋子中装有三个完全相同的小球，分别标有数字3、4、5．从袋子中随机取出一个小球，用小球上的数字作为十位的数字，然后放回；再取出一个小球，用小球上的数字作为个位上的数字，这样组成一个两位数，试问：按这种方法能组成哪些位数？十位上的数字与个位上的数字之和为9的两位数的概率是多少？用列表法或画树状图法加以说明．

【题目】（感知）如图①，在四边形ABCD中，点P在边AB上（点P不与点A、B重合），∠A＝∠B＝∠DPC＝90°．易证：△DAP∽△PBC（不要求证明）．

（探究）如图②，在四边形ABCD中，点P在边AB上（点P不与点A、B重合），∠A＝∠B＝∠DPC．

（1）求证：△DAP～△PBC．

（2）若PD＝5，PC＝10，BC＝9，求AP的长．

（应用）如图③，在△ABC中，AC＝BC＝4，AB＝6，点P在边AB上（点P不与点A、B重合），连结CP，作∠CPE＝∠A，PE与边BC交于点E．当CE＝3EB时，求AP的长．

【题目】已知：甲、乙两车分别从相距200千米的，两地同时出发相向而行，其中甲车到地后立即返回，下图是它们离各自出发地的距离（千米）与行驶时间（小时）之间的函数图象．

（1）求甲车离出发地的距离（千米）与行驶时间（小时）之间的函数关系式，并写出自变量的取值范围．

（2）当时，甲、乙两车离各自出发地的距离相等，求乙车离出发地的距离（千米）与行驶时间（小时）之间的函数关系式，并写出自变量的取值范围．

（3）在（2）的条件下，求它们在行驶的过程中相遇的时间．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网