��Ŀ����
����Ŀ����֪���ס��������ֱ�����200ǧ��![]() ��
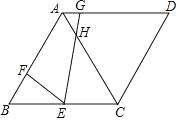
��![]() ����ͬʱ����������У����м׳���
����ͬʱ����������У����м׳���![]() �غ��������أ���ͼ����������Գ����صľ���
�غ��������أ���ͼ����������Գ����صľ���![]() ��ǧ�ף�����ʻʱ��
��ǧ�ף�����ʻʱ��![]() ��Сʱ��֮��ĺ���ͼ��
��Сʱ��֮��ĺ���ͼ��
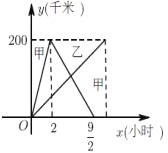
��1����׳�������صľ���![]() ��ǧ�ף�����ʻʱ��
��ǧ�ף�����ʻʱ��![]() ��Сʱ��֮��ĺ�����ϵʽ����д���Ա�����ȡֵ��Χ��
��Сʱ��֮��ĺ�����ϵʽ����д���Ա�����ȡֵ��Χ��
��2����![]() ʱ���ס�����������Գ����صľ�����ȣ����ҳ�������صľ���
ʱ���ס�����������Գ����صľ�����ȣ����ҳ�������صľ���![]() ��ǧ�ף�����ʻʱ��
��ǧ�ף�����ʻʱ��![]() ��Сʱ��֮��ĺ�����ϵʽ����д���Ա�����ȡֵ��Χ��
��Сʱ��֮��ĺ�����ϵʽ����д���Ա�����ȡֵ��Χ��
��3���ڣ�2���������£�����������ʻ�Ĺ�����������ʱ�䣮
���𰸡���1��![]()
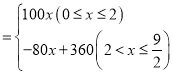 ����2��
����2��![]() ����3������
����3������![]() ��4Сʱ���ס�����������
��4Сʱ���ס�����������
��������
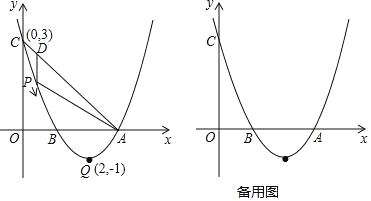
��1������ͼ���֪����0��x��2��2��x��![]() ���Σ����ô���ϵ�������һ�κ�������ʽ��
���Σ����ô���ϵ�������һ�κ�������ʽ��
��2�����ݣ�1�����������ʽ�����ֱ�ߵĽ������꣬�����ô���ϵ��������ҳ�������صľ���y��ǧ�ף�����ʻʱ��x��Сʱ��֮��ĺ�����ϵʽ��
��3����0��x��2��2��x��![]() ����������ֱ��г�������⼴�ɣ�
����������ֱ��г�������⼴�ɣ�
�⣺��1����0��x��2ʱ����y=mx��
��2m=200�����m=100��
���ԣ�y=100x��
��2��x��![]() ʱ����y=kx+b��
ʱ����y=kx+b��
��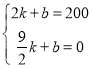 �����
�����![]() ��
��
��y=-80x+360��
��׳�������صľ���y��ǧ�ף�����ʻʱ��x��Сʱ��֮��ĺ�����ϵʽΪ�� 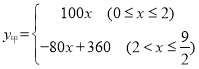 ��
��
��2����x=3ʱ��y��=-80��3+360=120��
��������ͼ�������Ϊ��3��120����
��y��=px��
����3��120�����룬��3p=120��
��ã�p=40��
���ҳ�������صľ���y��ǧ�ף�����ʻʱ��x��Сʱ��֮��ĺ�����ϵʽΪ��y��=40x��0��x��5����
��3���ٵ�![]() ʱ��������ã�
ʱ��������ã�![]() ��
��
��ã�![]() ��
��
�ڵ�![]() ʱ��������ã�
ʱ��������ã�![]() ��
��
��ã�![]() ��
��
�ྭ��![]() ��4Сʱ���ס�������������
��4Сʱ���ס�������������

����Ŀ����1����ij�ο����У����мס��ҡ���3��ͬѧ�����ĿƲ���ʵ�ʳɼ����±�������λ���֣�
���� | ��ѧ | Ӣ�� | ��ѧ | |
�� | 95 | 95 | 80 | 150 |
�� | 105 | 90 | 90 | 139 |
�� | 100 | 100 | 85 | 139 |
�������б���2�ˣ������ƽ�����ĽǶȷ����������˽������
��2��Ϊ�����ֿ�ѧ���죬������Ե����ġ���ѧ��Ӣ���ѧʵ�ʳɼ�����2:3:2:3�ı��������ۺ�ƽ������������ۺ�ƽ�����ĽǶȷ����������˽������