题目内容
 已知一次函数y=ax+b在坐标系中的图象如图,判断一次函数y=bx+a在坐标系中的大致图象是( )
已知一次函数y=ax+b在坐标系中的图象如图,判断一次函数y=bx+a在坐标系中的大致图象是( )A、 |
B、 |
C、 |
D、 |
考点:一次函数图象与系数的关系
专题:
分析:由y=ax+b的图象可知,a>0,b<0;所以一次函数y=bx+a在坐标系中的图象经过第二、四象限,且与y轴交于正半轴,由此根据图象选择答案即可.
解答:解:∵y=ax+b的图象经过第一、三、四象限,
∴a>0,b<0;
∴y=bx+a在坐标系中的图象经过第二、四象限,且与y轴交于正半轴,也就是经过第一、二、四象限,
符合条件的是D.
故选:D.
∴a>0,b<0;
∴y=bx+a在坐标系中的图象经过第二、四象限,且与y轴交于正半轴,也就是经过第一、二、四象限,
符合条件的是D.
故选:D.
点评:主要考查了一次函数的图象性质,要掌握它的性质才能灵活解题.一次函数y=kx+b的图象有四种情况:
①当k>0,b>0,函数y=kx+b的图象经过第一、二、三象限;
②当k>0,b<0,函数y=kx+b的图象经过第一、三、四象限;
③当k<0,b>0时,函数y=kx+b的图象经过第一、二、四象限;
④当k<0,b<0时,函数y=kx+b的图象经过第二、三、四象限.
①当k>0,b>0,函数y=kx+b的图象经过第一、二、三象限;
②当k>0,b<0,函数y=kx+b的图象经过第一、三、四象限;
③当k<0,b>0时,函数y=kx+b的图象经过第一、二、四象限;
④当k<0,b<0时,函数y=kx+b的图象经过第二、三、四象限.

练习册系列答案
相关题目
下列式子中,正确的是( )
| A、x2•x3=x6 |
| B、x6÷x2=x3 |
| C、x2+x3=x5 |
| D、(x2y)3=x6y3 |
下列计算正确的是( )
| A、x2•x3=x6 |
| B、(3xy)3=9x3y3 |
| C、(-2a2)2=-4a2 |
| D、(ab2)3=a3b6 |
 如图,AB∥CD,且CD=CB,∠D=70°,则∠ABC的度数为
如图,AB∥CD,且CD=CB,∠D=70°,则∠ABC的度数为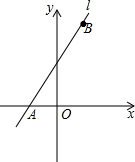 如图,已知直线l1经过点A(-1,0)和点B(1,4)
如图,已知直线l1经过点A(-1,0)和点B(1,4)