Question

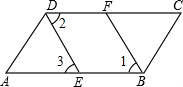已知，如图，∠ABC=∠ADC，BF、DE分别平分∠ABC与∠ADC，且∠1=∠3．求证：AB∥DC．
请根据条件进行推理，得出结论，并在括号内注明理由．
证明：∵BF、DE分别平分∠ABC与∠ADC，
∴∠1=∠ABC，∠2=．（________）
∵∠ABC=∠ADC，
∵∠________=∠________．
∵∠1=∠3，
∴∠2=________．（等量代换）
∴________∥________．（________）

Answer 1

角平分线定义    1    2    3    AB    CD    内错角相等，两直线平行
分析：根据几何证明题的格式和有关性质定理，填空即可．
解答：解∵BF、DE分别平分∠ABC与∠ADC，
∴∠1=∠ABC，∠2=．（角平分线定义 ）
∵∠ABC=∠ADC，
∵∠1=∠2．
∵∠1=∠3，
∴∠2=∠3．（等量代换）
∴AB∥CD．（内错角相等，两直线平行）
故答案为：角平分线定义；1；2；∠3；AB；CD；内错角相等，两直线平行．
点评：此题考查了平行线的判定与性质，用到的知识点是平行线的判定与性质、角平分线定义，要掌握几何证明题的格式，会注明理由．