Question

【题目】如图，在平行四边形ABCD中，BE⊥CD，BF⊥AD，垂足分别为E，F，CE＝2，DF＝1，∠EBF＝60°，则平行四边形ABCD的周长为_____．

Answer 1

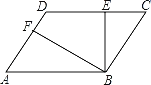
【答案】20

【解析】

由在平行四边形ABCD中，BE⊥CD，BF⊥AD，∠EBF＝60°，可求得∠ABF＝∠CBF＝30°，然后由CE＝2，DF＝1，利用含30°的直角三角形的性质，即可求得答案．

解：∵在平行四边形ABCD中，BE⊥CD，BF⊥AD，∠EBF＝60°，

∴∠AFB＝∠CEB＝90°，AD//CB，AB//CD，

∴∠CBF=∠AFB=90°，∠ABE=∠BEC=90°，

∴∠ABF=90°-∠EBF=30°，∠CBE=90°-∠EBF=30°，

∵在Rt△BCE中，CE＝2，

∴BC＝2CE＝4，

∴AD＝BC＝4，

∵DF＝1，

∴AF＝AD﹣DF＝3，

在Rt△ABF中，AB＝2AF＝6，

∴CD＝AB＝6，

∴平行四边形ABCD的周长为：2（AB+BC）＝2×（4+6）＝20，

故答案为：20．