Question

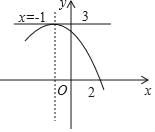
【题目】已知是平面直角坐标中的一点，点是轴负半轴上一动点，联结，并以为边在轴上方作矩形，且满足，设点的横坐标是，如果用含的代数式表示点的坐标，那么点的坐标是_____．

Answer 1

【答案】

【解析】

作辅助线,证明△BCH∽△ABF,求得,进而证明△BCH≌△ADE,求出AE=BH=1,DE=CH=,即可解题.

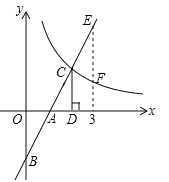
解：如图,过点C作CH⊥x轴于H,过A作AF⊥x轴于F,AG⊥y轴于G,过D作DE⊥AG于E,

∴∠CHB=∠AFO=∠AED=90°,

∴∠GAF=90°,∠DAE=∠FAB,

∵四边形ABCD是矩形,

∴∠ABC=90°,

∴∠BCH=∠ABF,

∴△BCH∽△ABF

∴,

∵A(3,2),

∴AF=2,AG=3,

∵点C的横坐标是a,

∴OH=-a,

∵BC：AB= 1: 2,

∴BH=,CH=,

∵△BCH∽△ABF

∴∠HBC=∠DAE,

在△BCH与△ADE中

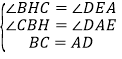
∴△BCH≌△ADE,

∴AE=BH=1,DE=CH=,

∴EG=3-1=2,

∴D.