题目内容
2.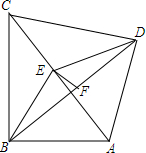 如图,∠ABC=∠ADC=90°,∠ACB=30°,∠DAC=45°,E是AC的中点,连结BE,DE,BD,F是BD的中点,连结EF.求∠BEF的度数.
如图,∠ABC=∠ADC=90°,∠ACB=30°,∠DAC=45°,E是AC的中点,连结BE,DE,BD,F是BD的中点,连结EF.求∠BEF的度数.
分析 根据直角三角形斜边上的中线等于斜边的一半可得BE=DE=$\frac{1}{2}$AC,再根据等腰三角形三线合一的性质即可得到结论.
解答 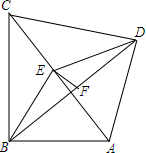 解:∵∠ABC=∠ADC=90°,E是AC的中点,
解:∵∠ABC=∠ADC=90°,E是AC的中点,
∴BE=DE=AE=$\frac{1}{2}$AC,
∵∠ACB=30°,∠DAC=45°,
∴∠BAC=∠AEB=60°,∠AED=90°,
∴∠BED=150°,
∴∠EBF=$\frac{1}{2}$(180°-∠BED)=15°,
∴F是BD的中点,
∴EF⊥BD,
∴∠BFE=90°,
∴∠BEF=75°.
点评 本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形三线合一的性质,熟记性质是解题的关键.

练习册系列答案
相关题目
10.若关于x的方程x2+3x+a=0有一个根为-1,则a的值为( )
| A. | -2 | B. | 2 | C. | 4 | D. | -3 |
 如图,边长分别为a,b的两个正方形拼在一起,试写出阴影部分的面积,并求出当a=5cm,b=3cm时,阴影部分的面积.
如图,边长分别为a,b的两个正方形拼在一起,试写出阴影部分的面积,并求出当a=5cm,b=3cm时,阴影部分的面积.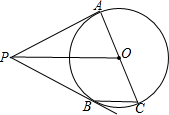 如图,已知P为⊙O外一点,PA、PB为⊙O的切线,切点为A、B,AC是直径.
如图,已知P为⊙O外一点,PA、PB为⊙O的切线,切点为A、B,AC是直径.