题目内容
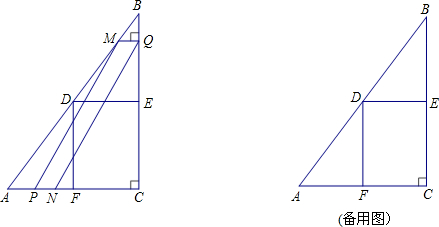
 (2013•吉林)如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为直角边作等腰三角形CDE,其中∠DCE=90°,连接BE.
(2013•吉林)如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为直角边作等腰三角形CDE,其中∠DCE=90°,连接BE.(1)求证:△ACD≌△BCE;
(2)若AC=3cm,则BE=
6
| 2 |
6
cm.| 2 |
分析:(1)求出∠ACD=∠BCE,根据SAS推出两三角形全等即可;
(2)根据全等得出AD=BE,根据勾股定理求出AB,即可求出AD,代入求出即可.
(2)根据全等得出AD=BE,根据勾股定理求出AB,即可求出AD,代入求出即可.
解答:(1)证明:∵△CDE是等腰直角三角形,∠DCE=90°,
∴CD=CE,
∵∠ACB=90°,
∴∠ACB=∠DCE,
∴∠ACB+∠BCD=∠DCE+∠BCD,
∴∠ACD=∠BCE,
在△ACD和△BCE中
,
∴△ACD≌△BCE;
(2)解:∵AC=BC=3,∠ACB=90°,由勾股定理得:AB=3
,
又∵DB=AB,
∴AD=2AB=6
,
∵△ACD≌△BCE;
∴BE=AD=6
,
故答案为:6
.
∴CD=CE,
∵∠ACB=90°,
∴∠ACB=∠DCE,
∴∠ACB+∠BCD=∠DCE+∠BCD,
∴∠ACD=∠BCE,
在△ACD和△BCE中
|
∴△ACD≌△BCE;
(2)解:∵AC=BC=3,∠ACB=90°,由勾股定理得:AB=3
| 2 |
又∵DB=AB,
∴AD=2AB=6
| 2 |
∵△ACD≌△BCE;
∴BE=AD=6
| 2 |
故答案为:6
| 2 |
点评:本题考查了等腰直角三角形性质,勾股定理,全等三角形的性质和判定的应用,主要考查学生运用定理进行推理的能力.

练习册系列答案
相关题目
 (2013•吉林)如图,把Rt△ABC绕点A逆时针旋转40°,得到Rt△AB′C′,点C′恰好落在边AB上,连接BB′,则∠BB′C′=
(2013•吉林)如图,把Rt△ABC绕点A逆时针旋转40°,得到Rt△AB′C′,点C′恰好落在边AB上,连接BB′,则∠BB′C′= (2013•吉林)如图所示,体育课上,小丽的铅球成绩为6.4m,她投出的铅球落在( )
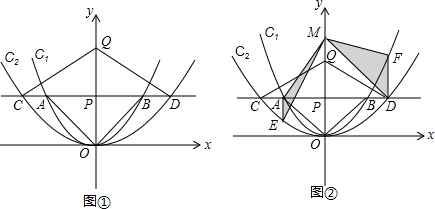
(2013•吉林)如图所示,体育课上,小丽的铅球成绩为6.4m,她投出的铅球落在( ) (2013•吉林)如图,在平面直角坐标系中,抛物线所表示的函数解析式为y=-2(x-h)2+k,则下列结论正确的是( )
(2013•吉林)如图,在平面直角坐标系中,抛物线所表示的函数解析式为y=-2(x-h)2+k,则下列结论正确的是( )