题目内容
如图,AB是⊙O的直径,AB=4,过点B作⊙O的切线,C是切线上一点,且BC=2,P是线段OA上一动点,连结PC交⊙O于点D,过点P作PC的垂线,交切线BC于点E,交⊙O于点F,连结DF交AB于点G.
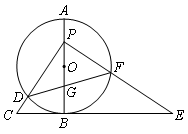
(1)当P是OA的中点时,求PE的长;
(2)若∠PDF=∠E,求△PDF的面积.

(1)当P是OA的中点时,求PE的长;
(2)若∠PDF=∠E,求△PDF的面积.
(1) ;(2)2或
;(2)2或 .
.
 ;(2)2或
;(2)2或 .
.试题分析:(1)当P是OA的中点时,根据切线的性质,可证得△CBP∽△PBE,从而得到
 ,在Rt△PBE中,由勾股定理可求得PE的长;(2)分弦DF不是直径和弦DF恰为直径两种情况讨论即可.
,在Rt△PBE中,由勾股定理可求得PE的长;(2)分弦DF不是直径和弦DF恰为直径两种情况讨论即可.试题解析:(1)当P是OA的中点时,PB=3.
∵CE是⊙O的切线,∴AB⊥CE.
又∵CP⊥PE,∠CPB=∠E,∴△CBP∽△PBE.
∴
 ,∴
,∴ .
.∴在Rt△PBE中,
 .
.(2)在Rt△PDG中,由∠PDF=∠E=∠CPB,可知∠GPF=∠GFP,
∴GD=GP=GF.
直径AB平分弦DF,有两种可能.:
①弦DF不是直径,如图①,则AB⊥DF,于是PD=PF,∠GPD=∠GDP=45º.
∴BP=BC=2=BO,点P与点O重合.∴S△PDF=
 ×2×2=2.
×2×2=2.②弦DF恰为直径,如图②,则点P即为点A.而BC=2,BP=DF=4,∴BE=8,CE=10.
∴S△PCE=
 ×10×4=20,∴由△PCE∽△PFD得,S△PDF=
×10×4=20,∴由△PCE∽△PFD得,S△PDF= .
.

练习册系列答案
相关题目

 对称的△A1B1C1,并写出点C1 的坐标;
对称的△A1B1C1,并写出点C1 的坐标; )
) ;
;

 是⊙O的直径, 点C在⊙O上,
是⊙O的直径, 点C在⊙O上, 交过点B的射线于D,交AB于F,且
交过点B的射线于D,交AB于F,且 .
.
 是⊙O的切线;(2)若
是⊙O的切线;(2)若 , 求⊙O的半径.
, 求⊙O的半径.

 是
是 的直径,
的直径, 、
、 、
、 都是
都是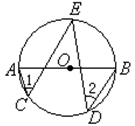
 ).
).