Question

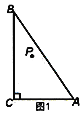
【题目】如图，在Rt△ABC中，∠B=90°，∠BAC=45°.

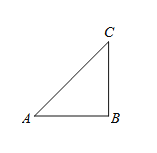
(1)尺规作图：

①在CA的延长线上截取AD=AB，并连结BD；

②在∠BAC内部作∠CAE=∠ABD，交BC边于点E；(保留作图痕迹，不写作法)

(2)求∠AEC的度数.

Answer 1

【答案】（1）见解析；（2）67.5°；

【解析】

（1）①延长CA，以点A为圆心，以AB的长为半径作圆，交CA的延长线于点D，则AD=AB；

②作∠CAE=∠ABD即可；

（2）先根据补角的定义得出∠BAD的度数，再由等腰三角形的性质求出∠DAB的度数，进而可得出∠EAC的度数，由三角形内角和定理即可得出结论．

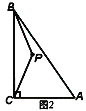
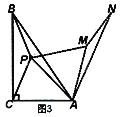
(1)①如图，AD=AB；

②如图，∠CAE即为所求；

(2)∵∠BAC=45°，

∴∠BAD=180°45°=135°.

∵AD=AB，

∴∠BAD==22.5°.

∵∠CAE=∠ABD=22.5°，

∴∠AEC=90°22.5°=67.5°.