题目内容
13. 如图,∠ABM为直角,点C为线段BA的中点,点D为射线BM上的一个动点(不与点B重合),连接AD,作BE⊥AD,垂足为E,连接CE,过点E作EF⊥CE,交BD于点F.
如图,∠ABM为直角,点C为线段BA的中点,点D为射线BM上的一个动点(不与点B重合),连接AD,作BE⊥AD,垂足为E,连接CE,过点E作EF⊥CE,交BD于点F.(1)求证:BF=EF;
(2)猜想四边形ACFE是什么特殊的四边形?并说明理由:
(3)∠A在什么范围内变化时,线段DE上存在一点G,满足条件DG=$\frac{1}{4}$DA?说明理由.
分析 (1)先根据直角三角形斜边上的中线等于斜边的一半得出CE=$\frac{1}{2}$AB=BC,得出∠CBE=∠CEB,证出∠FBE=∠FEB,即可得出结论;
(2)先证明CF垂直平分BE,证出CF∥AD,得出四边形ACFE是梯形;
(3)假设在线段DE上存在一点G;过G作GH⊥BD于点H,先证出DH=$\frac{1}{4}$BD=$\frac{1}{2}$DF,得出∠EDF=∠GFD=∠DEF,设∠A=x,则∠EDF=∠GFD=∠DEF=90°-x,而∠EDF+∠GFD+∠DEF≤∠EDF+∠EFD+∠DEF=180°,即可得出结果.
解答 (1)证明:∵BE⊥AD,
∴∠AEB=∠BED=90°,
∵点C为线段BA的中点,
∴CE=$\frac{1}{2}$AB=AC=BC,
∴∠CBE=∠CEB,
∵∠ABM=90°,
∴∠FBE=∠FEB,
∴BF=EF;
(2)解:四边形ACFE是梯形;
理由如下:由(1)得:CE=BC,BF=EF,
∴点C在BE的垂直平分线上,点F在BE的垂直平分线上,
∴CF垂直平分BE,
∴BE⊥CF,
∵BE⊥AD,
∴CF∥AD,
又∵CF<AD,
∴四边形ACFE是梯形;
(3)解:30°≤∠A<90°,假设在线段DE上存在一点G;
过G作GH⊥BD于点H,如图所示: 在Rt△BED中,∠DEF+∠FEB=90°,∠FBE+∠BDE=90°,
在Rt△BED中,∠DEF+∠FEB=90°,∠FBE+∠BDE=90°,
∴∠FBE=∠FEB,
∴∠DEF=∠BDE,
∴DF=EF,
∴BF=DF,即F为BD的中点,
∴DH=$\frac{1}{4}$BD=$\frac{1}{2}$DF,
∴∠EDF=∠GFD=∠DEF,
设∠A=x,则∠EDF=∠GFD=∠DEF=90°-x,
而∠EDF+∠GFD+∠DEF≤∠EDF+∠EFD+∠DEF=180°,
∴3(90°-x)≤180°
解得:x≥30°,
故30°≤∠A<90°.
点评 本题考查了等腰三角形的判定与性质、梯形的判定以及直角三角形斜边上的中线性质;根据题意弄清角之间的数量关系是解决问题的关键.

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
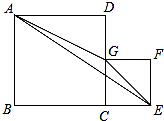 如图,正方形ABCD和正方形CEFG的边长分别为a,$\frac{a}{2}$.
如图,正方形ABCD和正方形CEFG的边长分别为a,$\frac{a}{2}$.
 已知△ABC,以BC、AC为边分别向外作正方形BCDE和正方形ACFG,连接FD.如图,求证:S△ABC=S△CDF.
已知△ABC,以BC、AC为边分别向外作正方形BCDE和正方形ACFG,连接FD.如图,求证:S△ABC=S△CDF.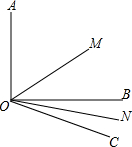 如图所示,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC;
如图所示,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC;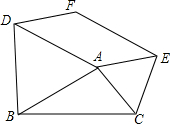 如图,分别以△ABC的边AB、AC为边向形外作正△ABD和正△ACE,且DF∥AE,EF∥AD.
如图,分别以△ABC的边AB、AC为边向形外作正△ABD和正△ACE,且DF∥AE,EF∥AD.