题目内容
如图，∠ACB=∠ADC=90°，AC=| 6 |
分析：欲证△ACB∽△ADC，通过观察发现两个三角形已经具备一组角对应相等，即∠ACB=∠CDA=90°，此时，再求夹此对应角的两边对应成比例即可．
解答：解：若△ACB∽△ADC，
∵∠ACB=∠ADC=90°，
需
=
，或
=
∵AC=
，AD=2，
∴CD=
∴AB=3，或AB=3
．
∵∠ACB=∠ADC=90°，
需
| AC |
| AD |
| AB |
| AC |
| AC |
| CD |
| AB |
| AC |
∵AC=
| 6 |
∴CD=
| 2 |
∴AB=3，或AB=3
| 2 |
点评：本题考查相似三角形的判定．识别两三角形相似，除了要掌握定义外，还要注意正确找出两三角形的对应边成比例、对应角相等．
练习册系列答案
相关题目
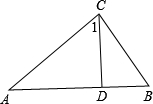如图，△ACB中，∠ACB=90°，∠1=∠B．
13、如图，∠ACB=90°，把Rt△ABC绕点A逆时针旋转90°得到Rt△AB1C1，若BC=1，AB=2，则∠CAB1的度数是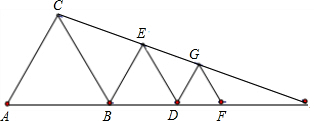
如图，△ACB、△BDE和△DGF都是等边三角形，且点E、G在△ABC边AB的延长线上，设等边的面积分别为S1、S2、S3，若S1=9，S3=1，则S2=
如图，∠ACB=90°，AC=BC，BE⊥CE于点E，AD⊥CE于D，AD=5cm，DE=2.3cm，则BE的长为
已知：如图，∠ACB=∠DBC，根据图形条件，若增加一个条件