题目内容
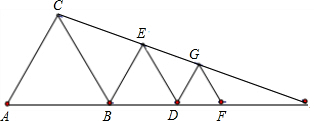如图，△ACB、△BDE和△DGF都是等边三角形，且点E、G在△ABC边AB的延长线上，设等边的面积分别为S1、S2、S3，若S1=9，S3=1，则S2=分析：由△ABC∽△BDE，得
=
，同理
=
，可证△CBE∽△EDG，得
=
，列等式求S2．
| BC |
| BE |
| ||
|
| ED |
| DG |
| ||
|
| BC |
| ED |
| BE |
| DG |
解答：解：△ABC和△BDE都是正三角形，所以△ABC∽△BDE，得
=
，
同理可得
=
，
可证△CBE∽△EDG，
得
=
，即
=
，
由此可得
=
，
=
，
可求得S2=3．
故本题答案为：3．
| BC |
| BE |
| ||
|
同理可得
| ED |
| DG |
| ||
|
可证△CBE∽△EDG，
得
| BC |
| ED |
| BE |
| DG |
| BC |
| BE |
| ED |
| DG |
由此可得
| ||
|
| ||
|
| ||
|
| ||
|
可求得S2=3．
故本题答案为：3．
点评：解决本题的关键是根据等边三角形的性质及相似三角形的判定与性质来得出等量关系．
练习册系列答案
备战中考寒假系列答案
相关题目
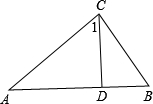如图，△ACB中，∠ACB=90°，∠1=∠B．
13、如图，∠ACB=90°，把Rt△ABC绕点A逆时针旋转90°得到Rt△AB1C1，若BC=1，AB=2，则∠CAB1的度数是
如图，∠ACB=90°，AC=BC，BE⊥CE于点E，AD⊥CE于D，AD=5cm，DE=2.3cm，则BE的长为
已知：如图，∠ACB=∠DBC，根据图形条件，若增加一个条件