题目内容
如图,矩形纸片ABCD中,AB=6,BC=8.折叠纸片使点B落在AD上,落点为B′.点B′从点A开始沿AD移动,折痕所在直线l的位置也随之改变,当直线l经过点A时,点B′停止移动,连接BB′.设直线l与AB相交于点E,与CD所在直线相交于点F,点B′的移动距离为x,点F与点C的距离为y.
(1)求证:∠BEF=∠AB′B;
(2)求y与x的函数关系式,并直接写出x的取值范围.

(1)证明:如图,由四边形ABCD是矩形和折叠的性质可知,BE=B′E,∠BEF=∠B′EF,
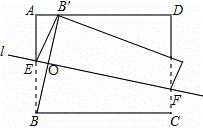
∴在等腰△BEB′中,EF是角平分线,
∴EF⊥BB′,∠BOE=90°,
∴∠ABB′+∠BEF=90°,
∵∠ABB′+∠AB′B=90°,
∴∠BEF=∠AB′B;
(2)解:①当点F在CD之间时,如图1,作FM⊥AB交AB于点E,

∵AB=6,BE=EB′,AB′=x,BM=FC=y,
∴在RT△EAB′中,EB′2=AE2+AB′2,
∴(6﹣AE)2=AE2+x2
解得AE= ,
,
tan∠AB′B= =,tan∠BEF=
=,tan∠BEF= =
=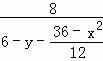 ,
,
∵由(1)知∠B EF=∠AB′B,
EF=∠AB′B,
∴=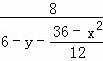 ,
,
化简,得y=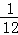 x2﹣x+3,(0<x≤8﹣2
x2﹣x+3,(0<x≤8﹣2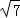 )
)
②当点F在点C下方时,如图2所示.
设直线EF与BC交于点K
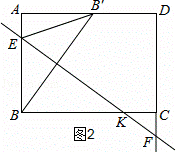
设∠ABB′=∠BKE=∠CKF=θ,则tanθ= =.
=.
BK=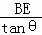 ,CK=BC﹣BK=8﹣
,CK=BC﹣BK=8﹣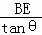 .
.
∴CF=CK•tanθ=(8﹣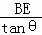 )•tanθ=8tanθ﹣BE=x﹣BE.
)•tanθ=8tanθ﹣BE=x﹣BE.
在Rt△EAB′中,EB′2=AE2+AB′2,
∴(6﹣BE)2+x2=BE2
解得BE= .
.
∴CF=x﹣BE=x﹣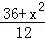 =﹣
=﹣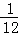 x2+x﹣3
x2+x﹣3
∴y=﹣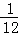 x2+x﹣3(8﹣2
x2+x﹣3(8﹣2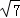 <x≤6)
<x≤6)
综上所述,
y= .
.

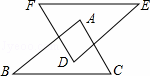
如图,AB∥DE,AC∥DF,AC=DF,下列条件中不能判断△ABC≌△DEF的是( )
|
| A. | AB=DE | B. | ∠B=∠E | C. | EF=BC | D. | EF∥BC |
贵阳市中小学幼儿园“爱心助残工程”第九届助残活动于2014年5月在贵阳市盲聋哑学校举行,活动当天,贵阳市盲聋哑学校获得捐赠的善款约为150000元.150000这个数用科学记数法表示为( )
|
| A. | 1.5×104 | B. | 1.5×105 | C. | 1.5×106 | D. | 15×104 |
如图,A点的坐标为(﹣4,0),直线y=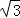 x+n与坐标轴交于点B,C,连接AC,如果∠ACD=90°,则n的值为( )
x+n与坐标轴交于点B,C,连接AC,如果∠ACD=90°,则n的值为( )
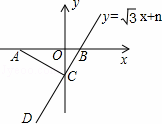
|
| A. | ﹣2 | B. | ﹣ | C. | ﹣ | D. | ﹣ |
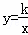 在第一象限内的图象交于点B(m,n),连结OB.若S△AOB=6,S△BOC=2.
在第一象限内的图象交于点B(m,n),连结OB.若S△AOB=6,S△BOC=2.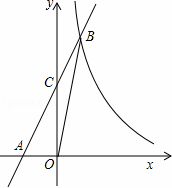










 ﹣2sin60°+|﹣
﹣2sin60°+|﹣ |.
|.