题目内容
18.计算:(1)$\left\{\begin{array}{l}{3x-2y=7}\\{x+2y=1}\end{array}\right.$
(2)1997×2003 (用简便方法)
(3)$\left\{\begin{array}{l}2x-y=3\\ 3x+2y=7\end{array}\right.$
(4)1992-398×203+2032.
分析 (1)(3)利用加减消元法进行解答;
(2)根据平方差公式求出即可;
(4)将398转化为2×199,然后利用完全平方公式进行解答即可.
解答 解:(1)$\left\{\begin{array}{l}{3x-2y=7①}\\{x+2y=1②}\end{array}\right.$,
由①+②,得
x=2 ③,
把③代入②得到:y=-$\frac{1}{2}$.
则原方程组的解为:$\left\{\begin{array}{l}{x=2}\\{y=-\frac{1}{2}}\end{array}\right.$;
(2)原式=(2000-3)×(2000+3)
=20002-32
=4000000-9
=3999991;
(3)$\left\{\begin{array}{l}{2x-y=3①}\\{3x+2y=7②}\end{array}\right.$.
由①×2+②得到:x=$\frac{13}{7}$③
把③代入①得到:y=$\frac{20}{7}$.
则原方程组的解为:$\left\{\begin{array}{l}{x=\frac{13}{7}}\\{y=\frac{20}{7}}\end{array}\right.$;
(4)1992-398×203+2032,
=1992-2×199×203+2032,
=(199-203)2,
=16.
点评 本题考查了解二元一次方程组,完全平方公式以及平方差公式.运用平方差公式计算时,关键要找相同项和相反项,其结果是相同项的平方减去相反项的平方.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
 由若干个相同的小立方体组成一个几何体,从其上面看到的平面图形如图所示,其中的数字表示在该位置上的小立方体的层数.请分别画出从正面和左面看这个几何体得到的平面图形.
由若干个相同的小立方体组成一个几何体,从其上面看到的平面图形如图所示,其中的数字表示在该位置上的小立方体的层数.请分别画出从正面和左面看这个几何体得到的平面图形.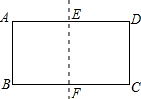 如图,将矩形ABCD沿两条长边中点的连线EF对折,如果矩形BFEA与矩形ABCD相似,求AB:AD的值.
如图,将矩形ABCD沿两条长边中点的连线EF对折,如果矩形BFEA与矩形ABCD相似,求AB:AD的值. 如图,已知中心线的两个半圆弧半径都为1000mm,两直管道的长度都为2000mm,求图中管道的展直长度(即图中虚线所表示的中心线的长度,精确到1mm)
如图,已知中心线的两个半圆弧半径都为1000mm,两直管道的长度都为2000mm,求图中管道的展直长度(即图中虚线所表示的中心线的长度,精确到1mm) 如图,在△ABC中,AD平分∠BAC,且$\frac{AD}{BD}$=$\frac{DC}{AD}$;若∠ADB=45°,求∠ACB的度数.
如图,在△ABC中,AD平分∠BAC,且$\frac{AD}{BD}$=$\frac{DC}{AD}$;若∠ADB=45°,求∠ACB的度数.