题目内容
3.如图1,四边形ABCD和四边形AEFG都是正方形.(1)连接DF和BF.求证:DF=BF;
(2)将正方形AEFG绕点A旋转一定角度(如图2),连接DG,在旋转过程中,你能找到与DG相等的线段吗?请加以证明.
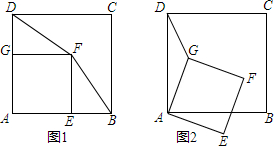
分析 (1)由正方形的性质得出AB=AD,∠A=∠AGF=∠AEF=90°,AG=AE=GF=EF,得出DG=BE,∠DGF=∠BEF=90°,由SAS证明△DGF≌△BEF,得出对应边相等即可;
(2)证出∠DAG=∠BAE,由SAS证明△ABE≌△ADG,得出对应边相等即可.
解答 (1)证明:如图1所示:
∵四边形ABCD和四边形AEFG都是正方形,
∴AB=AD,∠A=∠AGF=∠AEF=90°,AG=AE=GF=EF,
∴DG=BE,∠DGF=∠BEF=90°,
在△DGF和△BEF中,
$\left\{\begin{array}{l}{GF=EF}&{\;}\\{∠DGF=∠BEF}&{\;}\\{DG=BE}&{\;}\end{array}\right.$,
∴△DGF≌△BEF(SAS),
∴DF=BF;
(2)解:如图所示:BE=DG,理由如下:
根据题意得:∠BAD=∠EAG=90°,
∴∠DAG=∠BAE,
在△ABE和△ADG中,
$\left\{\begin{array}{l}{AB=AD}&{\;}\\{∠BAE=∠DAG}&{\;}\\{AE=AG}&{\;}\end{array}\right.$,
∴△ABE≌△ADG(SAS),
∴BE=DG.
点评 本题考查了正方形的性质、旋转的性质、全等三角形的判定与性质;熟练掌握正方形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案
相关题目
14.下列各对数中,数值相等的是( )
| A. | +32与+22 | B. | -23与(-2)3 | C. | -32与(-3)2 | D. | 3×22与(3×2)2 |
18.下列四个语句中正确的是( )
| A. | 如果AP=BP,那么点P是AB的中点 | B. | 两点间的距离就是两点间的线段 | ||
| C. | 两点之间,线段最短 | D. | 比较线段的长短只能用度量法 |
8.轮船航行到B处观测小岛A的方向是北偏西46°,那么从A同事观测轮船B的方向是( )
| A. | 南偏东46° | B. | 东偏北46° | C. | 东偏南46° | D. | 南偏东44° |
15.数轴上到原点距离等于5个单位长度的点所表示的数为( )
| A. | 5 | B. | -5 | C. | 5或-5 | D. | 以上都不对 |
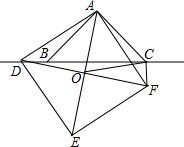 已知,如图,在Rt△ABC中,∠BAC=90°,∠ABC=45°,点D为直线BC上一
已知,如图,在Rt△ABC中,∠BAC=90°,∠ABC=45°,点D为直线BC上一 已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).