Question

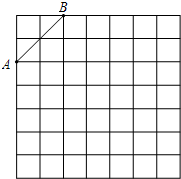如图，是7×7的正方形网格，请在所给网格中按下列要求操作：
（1）请在网格中建立平面直角坐标系，使A点坐标为（-4，2），B点坐标为（-2，4）．
（2）在第二象限内格点上找一点C，使C与线段AB 组成一个以AB为底的等腰三角形，且腰长是无理数，则C点坐标是

 

；△ABC周长是

 

．（结果保留根号）
（3）画出三角形ABC以O为位似中心，相似比为

1

2

的位似图形．

Answer 1

分析：（1）由于A点坐标为（-4，2），B点坐标为（-2，4），根据坐标和正方形网格即可确定坐标系；
（2）由于在第二象限内格点上找一点C，使C与线段AB 组成一个以AB为底的等腰三角形，且腰长是无理数，根据正方形网格和垂直平分线的性质即可确定C的坐标，接着确定△ABC周长；
（3）由于三角形ABC以O为位似中心，相似比为

1

2

的位似图形，那么此图形有两个，分别在第一三象限．

解答：解：（1）如图；
（2）C（-1，1）；
∵CA=CB=

1+32

=

10

，AB=

22+22

=2

2

，
∴△ABC周长是2

10

+2

2

；
（3）如图所示，
三角形ABC以O为位似中心，相似比为

1

2

的位似图形
为△A′B′C′和△A″B″C′″．

点评：本题考查了画位似图形及画三角形的内心．画位似图形的一般步骤为：
①确定位似中心；
②分别连接并延长位似中心和能代表原图的关键点；
③根据相似比，确定能代表所作的位似图形的关键点；顺次连接上述各点，得到放大或缩小的图形．