题目内容
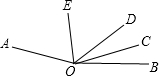 如图,已知∠AOB=160°,OD是∠AOB内任意一条射线,OE平分∠AOD,OC平分∠BOD.
如图,已知∠AOB=160°,OD是∠AOB内任意一条射线,OE平分∠AOD,OC平分∠BOD.(1)求∠EOC的度数;
(2)若∠BOC=19°,求∠EOD的度数.
考点:角平分线的定义
专题:
分析:(1)先根据角平分线定义得到∠EOD=
∠AOD,∠DOC=
∠DOB,再求出∠EOC=∠EOD+∠DOC=
∠AOB=80°;
(2)先根据角平分线定义得到∠DOB=2∠BOC=38°,再求出∠AOD=∠AOB-∠DOB=122°,然后根据角平分线定义得出∠EOD=
∠AOD=61°.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)先根据角平分线定义得到∠DOB=2∠BOC=38°,再求出∠AOD=∠AOB-∠DOB=122°,然后根据角平分线定义得出∠EOD=
| 1 |
| 2 |
解答:解:(1)∵OE平分∠AOD,OC平分∠BOD,
∴∠EOD=
∠AOD,∠DOC=
∠DOB,
∴∠EOC=∠EOD+∠DOC=
∠AOD+
∠DOB=
(∠AOD+∠DOB)=
∠AOB=80°;
(2)∵OC平分∠BOD,
∴∠DOB=2∠BOC=38°,
∴∠AOD=∠AOB-∠DOB=122°,
∵OE平分∠AOD,
∴∠EOD=
∠AOD=61°.
∴∠EOD=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠EOC=∠EOD+∠DOC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)∵OC平分∠BOD,
∴∠DOB=2∠BOC=38°,
∴∠AOD=∠AOB-∠DOB=122°,
∵OE平分∠AOD,
∴∠EOD=
| 1 |
| 2 |
点评:本题考查了角平分线定义和角的有关计算的应用,主要考查学生计算能力和推理能力,比较简单.

练习册系列答案
相关题目
 有理数a,b在数轴上对应的位置如图所示,则( )
有理数a,b在数轴上对应的位置如图所示,则( )| A、|a|=|b| |
| B、ab>0 |
| C、a+b<0 |
| D、a-b>0 |
下列命题:①若a>b>0,则以2
,a-b,a+b为三边的三角形是直角三角形;②两条弧的长度相等,它们是等弧;③等边三角形是轴对称图形,但不是中心对称图形;④有两边和第三边上的高对应相等的两个三角形全等.其中假命题的个数是( )
| ab |
| A、1个 | B、2个 | C、3个 | D、4个 |
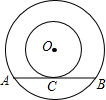 如图,以O为圆心的两个同心圆中,大圆的弦AB与小圆相切于点C,若大圆半径为10cm,小圆半径为6cm,则弦AB的长为( )
如图,以O为圆心的两个同心圆中,大圆的弦AB与小圆相切于点C,若大圆半径为10cm,小圆半径为6cm,则弦AB的长为( )| A、2cm | B、4cm |
| C、8cm | D、16cm |