题目内容
如图,同心⊙O,大⊙O的直径AB=2 ,小⊙O的直径CD=2,连接AC、AD、BD、BC,AD、CB分别交小⊙O于E、F.
,小⊙O的直径CD=2,连接AC、AD、BD、BC,AD、CB分别交小⊙O于E、F.
1.问四边形CEDF是何种特殊四边形?请证明你的结论;
2.当AC与小⊙O相切时,四边形CEDF是正方形吗?请说明理由.

【答案】
1.(1)四边形CEDF是矩形.
证明:∵CD是小⊙O的直径,∴∠CFD=∠CED=90°,
又∵AB、CD分别是大⊙O、小⊙O的直径,
∴OC=OD,OA=OB,
∴四边形ADBC是平行四边形,
∴CB∥AD,
∴∠CFD+∠EDF=180°,
∴∠EDF=90°,
∴四边形CEDF是矩形.
2.四边形CEDF是正方形.
理由:∵AC是小⊙O的切线,CD是直径,
∴∠ACD=90°,
在Rt△ACO中,OA= ,OC=1,
,OC=1, 5,∴AC=2,
5,∴AC=2,
则CD=AC=2,∠CDE=45°,
∴DE=CE,
∴矩形CEDF是正方形.
【解析】略

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
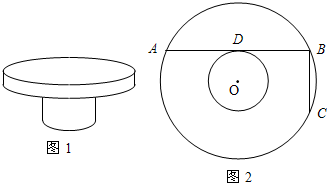
 ,小⊙O的直径CD=2,连接AC、AD、BD、BC,AD、CB分别交小⊙O于E、F.
,小⊙O的直径CD=2,连接AC、AD、BD、BC,AD、CB分别交小⊙O于E、F.
 ,小⊙O的直径CD=2,连接AC、AD、BD、BC,AD、CB分别交小⊙O于E、F.
,小⊙O的直径CD=2,连接AC、AD、BD、BC,AD、CB分别交小⊙O于E、F.
 ,小⊙O的直径CD=2,连接AC、AD、BD、BC,AD、CB分别交小⊙O于E、F.
,小⊙O的直径CD=2,连接AC、AD、BD、BC,AD、CB分别交小⊙O于E、F.