Question

【题目】阅读材料，解答问题：

（1）中国古代数学著作《周髀算经》有着这样的记载：“勾广三，股修四，经隅五．”这句话的意思是：“如果直角三角形两直角边为3和4时，那么斜边的长为5．”上述记载说明：在中，如果，，，，那么三者之间的数量关系是： ．

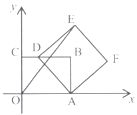
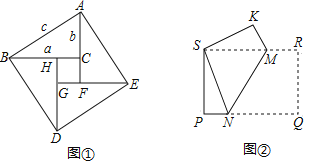
（2）对于（1）中这个数量关系，我们给出下面的证明．如图①，它是由四个全等的直角三角形围成的一个大正方形，中空的部分是一个小正方形．结合图①，将下面的证明过程补充完整：

∵，

（用含的式子表示）

又∵ ．

∴

∴

∴ ．

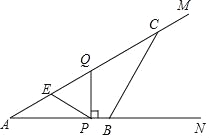
（3）如图②，把矩形折叠，使点与点重合，点落在点处，折痕为．如果，求的长．

Answer 1

【答案】（1）；（2）；正方形ABCD的面积；四个全等直角三角形的面积正方形CFGH的面积；；（3）3.

【解析】

（1）根据勾股定理解答即可；

（2）根据题意、结合图形，根据完全平方公式进行计算即可；

（3）根据翻折变换的特点、根据勾股定理列出方程，解方程即可．

解：（1）在中，，，，，
由勾股定理得，，
故答案为：；

（2），
又正方形的面积四个全等直角三角形的面积的面积正方形CFGH的面积，
．
．
，
故答案为：；正方形的面积；四个全等直角三角形的面积的面积正方形CFGH的面积；；

（3）设，则，
由折叠的性质可知，，
在中，，
则，
解得，，
则PN的长为3．