题目内容
16.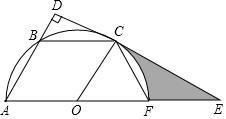 如图,已知平行四边形OABC的三个顶点A、B、C在以O为圆心的半圆上,过点C作CD⊥AB,分别交AB、AO的延长线于点D、E,AE交半圆O于点F,连接CF.
如图,已知平行四边形OABC的三个顶点A、B、C在以O为圆心的半圆上,过点C作CD⊥AB,分别交AB、AO的延长线于点D、E,AE交半圆O于点F,连接CF.(1)判断直线DE与半圆O的位置关系,并说明理由;
(2)①求证:CF=OC;
②若半圆O的半径为12,求阴影部分的周长.
分析 (1)结论:DE是⊙O的切线.首先证明△ABO,△BCO都是等边三角形,再证明四边形BDCG是矩形,即可解决问题;
(2)①只要证明△OCF是等边三角形即可解决问题;
②求出EC、EF、弧长CF即可解决问题.
解答 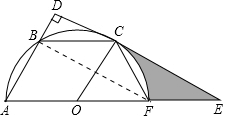 解:(1)结论:DE是⊙O的切线.
解:(1)结论:DE是⊙O的切线.
理由:∵CD⊥AD,
∴∠D=90°,
∵四边形OABC是平行四边形,
∴AD平行OC,
∴∠D=∠OCE=90°,
∴CO⊥DE,
∴DE是⊙O的切线.
(2)①连接BF.
∵四边形OABC是平行四边形,
∴BC∥AF,AB=OC,
∴∠AFB=∠CBF,
∴$\widehat{AB}$=$\widehat{CF}$,
∴AB=CF,
∴CF=OC.
②在Rt△OCE中,∵OC=12,∠COE=60°,∠OCE=90°,
∴OE=2OC=24,EC=12$\sqrt{3}$,
∵OF=12,
∴EF=12,
∴$\widehat{CF}$的长=$\frac{60π•12}{180}$=4π,
∴阴影部分的周长为4π+12+12$\sqrt{3}$.
点评 本题考查切线的判定、平行四边形的性质、等边三角形的判定和性质、弧长公式,解直角三角形等知识,解题的关键是学会添加常用辅助线,证明三角形是等边三角形是解题的突破点,属于中考常考题型.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
4.下列运算中,正确的是( )
| A. | (x+1)2=x2+1 | B. | (x2)3=x5 | C. | 2x4•3x2=6x8 | D. | x2÷x-1=x3(x≠0) |
8.估计$\sqrt{38}$的值在( )
| A. | 4和5之间 | B. | 5和6之间 | C. | 6和7之间 | D. | 7和8之间 |
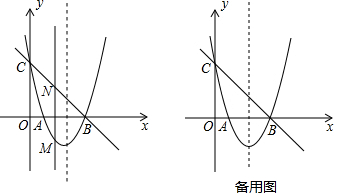
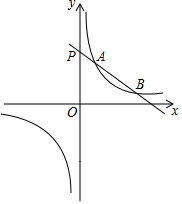 如图,反比例函数y=$\frac{m}{x}$的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1),且与y轴交于点P.
如图,反比例函数y=$\frac{m}{x}$的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1),且与y轴交于点P.