题目内容
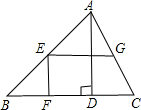 如图所示.△ABC中,AD⊥BC于点D,点E、F、G分别是AB、BD、AC的中点,若EG=
如图所示.△ABC中,AD⊥BC于点D,点E、F、G分别是AB、BD、AC的中点,若EG=| 3 | 2 |
分析:先根据EF是△ABD的中位线和AD+EF=12求出AD、EF的长度,再根据EG=
EF求出EG的长度,根据三角形的中位线平行于第三边并且等于第三边的一半即可求出底边BC的长度,代入三角形面积公式求解即可.
| 3 |
| 2 |
解答:解:∵点E、F分别是AB、BD的中点,
∴AD=2EF,
∵AD+EF=12,
∴AD=8,EF=4,
∵EG=
EF,
∴EG=
×4=6,
∵点E、G分别是AB、AC的中点,
∴BC=2EG=2×6=12,
∵AD⊥BC于点D,
∴S△ABC=
BC×AD=
×12×8=48.
∴AD=2EF,
∵AD+EF=12,
∴AD=8,EF=4,
∵EG=
| 3 |
| 2 |
∴EG=
| 3 |
| 2 |
∵点E、G分别是AB、AC的中点,
∴BC=2EG=2×6=12,
∵AD⊥BC于点D,
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要利用三角形的中位线定理求解,熟练掌握三角形中位线定理是解题的关键.

练习册系列答案
相关题目
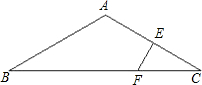 如图所示,△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.求证:BF=2CF.
如图所示,△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.求证:BF=2CF. 16、如图所示,△ABC中,∠C=90°,DE垂直平分斜边AB,分别交AB、AC于D、E,∠CAE:∠EAB=5:2,则∠B=
16、如图所示,△ABC中,∠C=90°,DE垂直平分斜边AB,分别交AB、AC于D、E,∠CAE:∠EAB=5:2,则∠B= 如图所示,△ABC中,AB=AC=10,BD是AC边的高线,DC=2,试求BD的长.
如图所示,△ABC中,AB=AC=10,BD是AC边的高线,DC=2,试求BD的长. 如图所示,△ABC中,BC的垂直平分线交AB于点E,若△ABC的周长为10,BC=4,则△ACE的周长是
如图所示,△ABC中,BC的垂直平分线交AB于点E,若△ABC的周长为10,BC=4,则△ACE的周长是 如图所示,△ABC中,AB=AC,BD⊥AC,垂足为D,求∠DBC与∠A的关系.
如图所示,△ABC中,AB=AC,BD⊥AC,垂足为D,求∠DBC与∠A的关系.