题目内容
 如图,⊙O与∠BAC的两边分别相切于点B、点C,已知∠BAC=60°,AB=
如图,⊙O与∠BAC的两边分别相切于点B、点C,已知∠BAC=60°,AB= 米,则⊙O的直径为________米.
米,则⊙O的直径为________米.
2
分析:由⊙O与∠BAC的两边分别相切于点B、点C,可得∠OAB= ∠BAC=
∠BAC= ×60°=30°,OB⊥AB,然后由三角函数的性质,求得OB的长,继而求得答案.
×60°=30°,OB⊥AB,然后由三角函数的性质,求得OB的长,继而求得答案.
解答:∵⊙O与∠BAC的两边分别相切于点B、点C,
∴∠OAB= ∠BAC=
∠BAC= ×60°=30°,OB⊥AB,
×60°=30°,OB⊥AB,
∵AB= 米,
米,
∴OB=AB•tan∠OAB= ×
× =1(米),
=1(米),
∴⊙O的直径为2米.
故答案为:2.
点评:此题考查了切线的性质、切线长定理以及三角函数的知识.此题难度不大,注意掌握数形结合思想的应用.
分析:由⊙O与∠BAC的两边分别相切于点B、点C,可得∠OAB=
 ∠BAC=
∠BAC= ×60°=30°,OB⊥AB,然后由三角函数的性质,求得OB的长,继而求得答案.
×60°=30°,OB⊥AB,然后由三角函数的性质,求得OB的长,继而求得答案.解答:∵⊙O与∠BAC的两边分别相切于点B、点C,
∴∠OAB=
 ∠BAC=
∠BAC= ×60°=30°,OB⊥AB,
×60°=30°,OB⊥AB,∵AB=
 米,
米,∴OB=AB•tan∠OAB=
 ×
× =1(米),
=1(米),∴⊙O的直径为2米.
故答案为:2.
点评:此题考查了切线的性质、切线长定理以及三角函数的知识.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,△ABC与△ADE均为等腰直角三角形,∠BAC=∠EAD=90°.求证:△BAE≌△CAD.
如图,△ABC与△ADE均为等腰直角三角形,∠BAC=∠EAD=90°.求证:△BAE≌△CAD.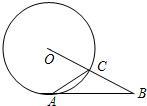
 如图,⊙O与∠BAC的两边分别相切于点B、点C,已知∠BAC=60°,AB=
如图,⊙O与∠BAC的两边分别相切于点B、点C,已知∠BAC=60°,AB= 如图,已知∠BAC的平分线与△ABC的边BC和外接圆分别相交于D、E.
如图,已知∠BAC的平分线与△ABC的边BC和外接圆分别相交于D、E.