题目内容
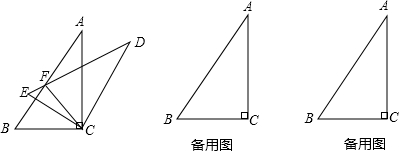
4.已知,△ABC和△DEC中,AC⊥BC,DC⊥EC,垂足均为点C,将△ABC绕着点C旋转得到△DEC,直线AB与直线DE交于点F(1)如图,若∠BCE=30°,求∠AFC的度数;
(2)若∠BCE=80°,请画出图形,求∠AFC的度数;
(3)若∠BCE=120°,请画出图形,求∠AFC的度数.
分析 (1)在BF上截取BG=EF,证明△BGC≌△EFC,得到△FCG为等腰三角形,证明∠FCG=30°,得到∠AFC的度数;
(2)画出图形,与(1)的作法相同,求出∠AFC的度数;
(3)根据题意画出图形,与(1)的作法相同,求出∠AFC的度数.
解答 解 :(1)如图1,在BF上截取BG=EF,
:(1)如图1,在BF上截取BG=EF,
在△BGC和△EFC中,
$\left\{\begin{array}{l}{BG=EF}\\{∠B=∠E}\\{BC=EC}\end{array}\right.$,
∴△BGC≌△EFC,
∴CG=CF,∠FCE=∠GCB,又∠BCE=30°,
∴∠FCG=30°,∴∠CFG=75°,
∴∠AFC=105°;
(2)如图2,延长AB至G,使BG=CF,连接CG,
由(1)得,∴△BGC≌△EFC,
∴CG=CF,∠FCE=∠GCB,又∠BCE=80°,
∴∠FCG=80°,∴∠CFG=50°,
∴∠AFC=130°;
(3) 如图3,延长AB至G,使BG=CF,连接CG
如图3,延长AB至G,使BG=CF,连接CG
由(1)得,∴△BGC≌△EFC,
∴CG=CF,∠FCE=∠GCB,又∠BCE=120°,
∴∠FCG=120°,
∴∠AFC=30°.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.

练习册系列答案
相关题目
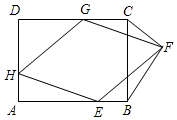 已知,如图,矩形ABCD中,AD=6,DC=10,菱形EFGH的三个顶点E,G,H分别在矩形ABCD的边AB,CD,DA上,AH=2,连接CF、BF.
已知,如图,矩形ABCD中,AD=6,DC=10,菱形EFGH的三个顶点E,G,H分别在矩形ABCD的边AB,CD,DA上,AH=2,连接CF、BF.
 如图,BC⊥ED,垂足为点O,∠A=28°,∠B=36°,求∠D的度数.
如图,BC⊥ED,垂足为点O,∠A=28°,∠B=36°,求∠D的度数.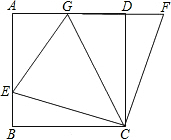 如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,G在AD上,且DF=BE.①CE=CF;②EC⊥CF;③△ECG≌△FCG,④若∠GCE=45°,则EG=BE+GD,以上说法正确的是①②④.
如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,G在AD上,且DF=BE.①CE=CF;②EC⊥CF;③△ECG≌△FCG,④若∠GCE=45°,则EG=BE+GD,以上说法正确的是①②④.



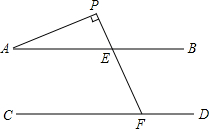 如图,直线AB∥CD,∠P=90°,试求∠EFD-∠A的度数,并写出每一步的依据.
如图,直线AB∥CD,∠P=90°,试求∠EFD-∠A的度数,并写出每一步的依据.