题目内容
在一条笔直的河道上依次有A、B、C三个港口,甲、乙两船同时分别从A、B 港口出发,沿直线匀速驶向C港,最终到达C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示(点P、Q为图象的交点).
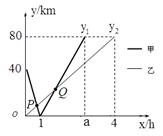
(1)填空:A、C两港口间的距离为 km,a= ;
(2)求y1与x的函数关系式,并写出自变量x的取值范围;
(3)求图中点P的坐标,并解释该点坐标所表示的实际意义。
(1)120,3;(2) ;
;
(3) ,当行驶
,当行驶 小时时,甲、乙两船到B港的距离都是
小时时,甲、乙两船到B港的距离都是 km
km
【解析】
试题分析:(1)从图象可以看出A、C两港口间的距离为A、B间的距离+B、C间的距离就可以求出结论;根据A、B之间的距离和行驶时间可以求出其速度,就可以求出从B到C的时间,从而求出a;
(2)当 时,设
时,设 ,根据图象过点(0,40),(1,0)可根据待定系数法求得函数关系式;当
,根据图象过点(0,40),(1,0)可根据待定系数法求得函数关系式;当 时,设
时,设 ,根据图象过点(1,0),(3,80)可根据待定系数法求得函数关系式;
,根据图象过点(1,0),(3,80)可根据待定系数法求得函数关系式;
(3)先求出直线y2的解析式,然后与 时对应的y1的解析式购成方程组求出其解就可以得出答案,此点表示甲乙两车相遇时离B港口的距离.
时对应的y1的解析式购成方程组求出其解就可以得出答案,此点表示甲乙两车相遇时离B港口的距离.
(1)由图象可得A、B之间的距离为40km,B、C之间的距离为80km,
∴A、C两港口间的距离为40+80=120km,
∵40÷1=40,
∴80÷40=2,
∴a=2+1=3;
(2)当 时,设
时,设
∵图象过点(0,40),(1,0)
 ,解得
,解得
∴函数关系式为
当 时,设
时,设
∵图象过点(1,0),(3,80)
 ,解得
,解得
∴函数关系式为
∴ ;
;
(3)设直线y2的解析式为
∵图象过点(4,80)
 ,
, 
∴函数关系式为
由 解得
解得
∴P点坐标为 ,表示当行驶
,表示当行驶 小时时,甲、乙两船到B港的距离都是
小时时,甲、乙两船到B港的距离都是 km.
km.
考点:一次函数的应用
点评:解答本题的关键是读懂题意,熟练掌握根据时间=路程÷速度求点的坐标的运用,同时熟记待定系数法求函数关系式.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案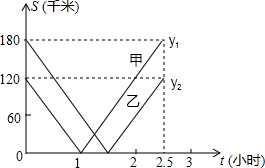 一条笔直的公路上依次有B、A、C三地,BC两地相距300千米,甲、乙两辆汽车分别从B、C两地同时出发,沿公路匀速相向而行,分别驶往C、B两地,甲、乙两车到A地的距离y1、y2(千米)与行驶时间t(时)的关系如图所示,则甲、乙两车相遇时离A地的距离为
一条笔直的公路上依次有B、A、C三地,BC两地相距300千米,甲、乙两辆汽车分别从B、C两地同时出发,沿公路匀速相向而行,分别驶往C、B两地,甲、乙两车到A地的距离y1、y2(千米)与行驶时间t(时)的关系如图所示,则甲、乙两车相遇时离A地的距离为
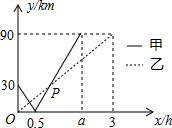 在一条笔直的河道上依次有A,B,C,三个港口在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终达到C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图.
在一条笔直的河道上依次有A,B,C,三个港口在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终达到C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图.