Question

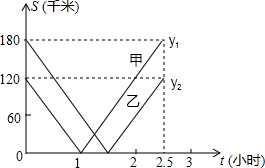一条笔直的公路上依次有B、A、C三地，BC两地相距300千米，甲、乙两辆汽车分别从B、C两地同时出发，沿公路匀速相向而行，分别驶往C、B两地，甲、乙两车到A地的距离y₁、y₂（千米）与行驶时间t（时）的关系如图所示，则甲、乙两车相遇时离A地的距离为

30

千米．

Answer 1

分析：由图象可知，甲、乙两辆汽车的速度相同，都是每小时120千米，再根据时间=路程÷速度，求出两车相遇的时间，然后得出甲车行驶的路程，进而求出甲、乙两车相遇时离A地的距离．

解答：解：∵甲车2.5小时行驶300千米，乙车2.5小时行驶300千米，
∴甲、乙两辆汽车的行驶速度=300÷2.5=120千米/时，
∴甲、乙两辆汽车分别从B、C两地同时出发，沿公路匀速相向而行时，相遇时间=

300

120+120

=

5

4

小时，
∴甲车行驶的路程=120×

5

4

=150千米，
∵出发时甲车距A地120千米，
∴甲、乙两车相遇时距A地150-120=30千米．
故答案为30．

点评：本题主要考查利用一次函数的模型解决实际问题的能力和读图能力，解题的关键是会根据图示得出所需要的信息．