题目内容
 一次函数y=ax+b的图象分别与x轴、y轴交于点M,N,与反比例函数y=
一次函数y=ax+b的图象分别与x轴、y轴交于点M,N,与反比例函数y=| k |
| x |
CD.若点A,B在反比例函数y=
| k |
| x |
(1)S四边形AEDK
=
=
S四边形CFBK(选择“<、=、>”填空),并写出上述关系的验证过程;(2)求证:△AKB∽△CKD;
(3)求证:BN=AM.
分析:(1)根据反比例函数的比例系数k的几何意义得到S矩形AEOC=k,S矩形BDOF=k,则S矩形AEOC-S矩形ODKC=S矩形BDOF-S矩形ODKC,所以S四边形AEDK=S四边形CFBK;
(2)由于S四边形AEDK=S四边形CFBK,根据矩形的面积公式得到KD•KA=KC•KB,变形为
=
,又∠CKD=∠AKB=90°,根据相似三角形的判定方法即可得到△AKB∽△CKD;
(3)由于△AKB∽△CKD,根据相似的性质得∠KCD=∠KAB,根据平行线的判定方法得DC∥AB,则易得四边形ACDN、四边形BDCM都是平行四边形,利用平行四边形的性质得AN=DC,BM=DC,所以AN=BM,然后根据等量代换即可得到BN=AM.
(2)由于S四边形AEDK=S四边形CFBK,根据矩形的面积公式得到KD•KA=KC•KB,变形为
| KD |
| KB |
| KC |
| KA |
(3)由于△AKB∽△CKD,根据相似的性质得∠KCD=∠KAB,根据平行线的判定方法得DC∥AB,则易得四边形ACDN、四边形BDCM都是平行四边形,利用平行四边形的性质得AN=DC,BM=DC,所以AN=BM,然后根据等量代换即可得到BN=AM.
解答:(1)解: ∵AC⊥x轴,AE⊥y轴,BF⊥x轴,BD⊥y轴,
∵AC⊥x轴,AE⊥y轴,BF⊥x轴,BD⊥y轴,
∴S矩形AEOC=k,S矩形BDOF=k,
∴S矩形AEOC=S矩形BDOF,
∴S矩形AEOC-S矩形ODKC=S矩形BDOF-S矩形ODKC,
∴S四边形AEDK=S四边形CFBK;
(2)证明:∵S四边形AEDK=S四边形CFBK,
∴KD•KA=KC•KB,即
=
,
∵∠CKD=∠AKB=90°,
∴△AKB∽△CKD;
(3)∵△AKB∽△CKD,
∴∠KCD=∠KAB,
∴DC∥AB,
∵AC∥DN,BD∥CM,
∴四边形ACDN、四边形BDCM都是平行四边形,
∴AN=DC,BM=DC,
∴AN=BM,
∴BN=AM.
故答案为:=.
 ∵AC⊥x轴,AE⊥y轴,BF⊥x轴,BD⊥y轴,
∵AC⊥x轴,AE⊥y轴,BF⊥x轴,BD⊥y轴,∴S矩形AEOC=k,S矩形BDOF=k,
∴S矩形AEOC=S矩形BDOF,
∴S矩形AEOC-S矩形ODKC=S矩形BDOF-S矩形ODKC,
∴S四边形AEDK=S四边形CFBK;
(2)证明:∵S四边形AEDK=S四边形CFBK,
∴KD•KA=KC•KB,即
| KD |
| KB |
| KC |
| KA |
∵∠CKD=∠AKB=90°,
∴△AKB∽△CKD;
(3)∵△AKB∽△CKD,
∴∠KCD=∠KAB,
∴DC∥AB,
∵AC∥DN,BD∥CM,
∴四边形ACDN、四边形BDCM都是平行四边形,
∴AN=DC,BM=DC,
∴AN=BM,
∴BN=AM.
故答案为:=.
点评:本题考查了反比例函数的综合题:掌握反比例函数图象上点的坐标特征、比例系数的几何意义和矩形和平形四边形的判定与性质;熟练运用相似三角形的判定与性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
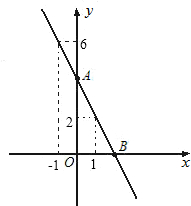 已知如图,一次函数y=ax+b图象经过点(1,2)、点(-1,6).求:
已知如图,一次函数y=ax+b图象经过点(1,2)、点(-1,6).求: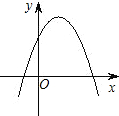 已知二次函数y=ax2+bx+c的图象如图所示,则在同一坐标系中,一次函数y=ax+c和反比例函数y=
已知二次函数y=ax2+bx+c的图象如图所示,则在同一坐标系中,一次函数y=ax+c和反比例函数y=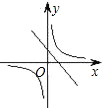
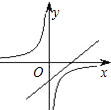
 如图,一次函数y=ax+b的图象与反比例函数y=
如图,一次函数y=ax+b的图象与反比例函数y=