题目内容
等腰三角形的顶角A=120°,底边BC的长为12cm,那么它的腰长是
- A.
 cm
cm - B.
 cm
cm - C.
 cm
cm - D.6cm
B
分析:根据ABC是等腰三角形和∠A的度数求出∠B、∠C的度数,设AD为x,根据在直角三角形中30°所对的直角边等于斜边的一半得出AB=2x,再根据勾股定理求出x的值,即可求出三角形的腰长.
解答: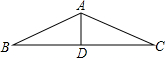 解:如图:
解:如图:
∵△ABC是等腰三角形,∠A=120°,
∴∠B=∠C=30°,AD⊥BC,
∵BC=12,
∴BD=6,
设AD为x,则AB=2x,根据勾股定理得:
AB2=AD2+BD2,即(2x)2=62+x2,
解得:x=2 ,
,
∴2x=4 ,
,
∴它的腰长是4 .
.
故选B.
点评:此题考查了解直角三角形,关键是根据题意画出图形,根据在直角三角形中30°所对的直角边等于斜边的一半得出AB与AD的关系.
分析:根据ABC是等腰三角形和∠A的度数求出∠B、∠C的度数,设AD为x,根据在直角三角形中30°所对的直角边等于斜边的一半得出AB=2x,再根据勾股定理求出x的值,即可求出三角形的腰长.
解答:
 解:如图:
解:如图:∵△ABC是等腰三角形,∠A=120°,
∴∠B=∠C=30°,AD⊥BC,
∵BC=12,
∴BD=6,
设AD为x,则AB=2x,根据勾股定理得:
AB2=AD2+BD2,即(2x)2=62+x2,
解得:x=2
 ,
,∴2x=4
 ,
,∴它的腰长是4
 .
.故选B.
点评:此题考查了解直角三角形,关键是根据题意画出图形,根据在直角三角形中30°所对的直角边等于斜边的一半得出AB与AD的关系.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目